
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы решения симметрических системы уравнений
|
|
В ряде случаев приходится решать системы уравнений с симметрическим вхождением слагаемых или сомножителей. Системы с таким свойством будем называть симметрическими. К таким системам относятся системы вида
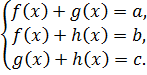 (9.1)
(9.1)
и
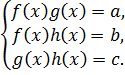 (9.2)
(9.2)
Метод решения системы (9.1) состоит в сложении левых и правых частей уравнений. Тогда
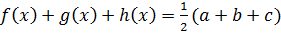 ,
,
Заем из полученного уравнения поочередно вычитываются третье, второе и первое уравнения системы (9.1), в результате чего получается система уравнений
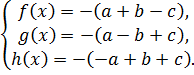 (9.3)
(9.3)
При решении системы уравнений (9.2) необходимо перемножить левые и правые части уравнений, тогда получаем
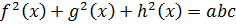 и
и 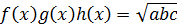 .
.
Здесь необходимо потребовать, чтобы выполнялось условие 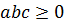 . Если затем полученное уравнение разделить поочередно на третье, второе и первое уравнения системы (9.2), то получаем две системы уравнений относительно
. Если затем полученное уравнение разделить поочередно на третье, второе и первое уравнения системы (9.2), то получаем две системы уравнений относительно 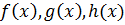 вида
вида
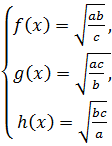 и
и 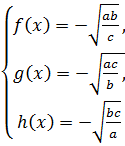 (9.4)
(9.4)
Полученные системы уравнений относительно 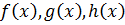 допускают более простое решение по сравнению с решением систем уравнений (9.1), (9.2). Следует отметить, что данный метод обобщается на случай произвольного числа уравнений, содержащихся симметрических системах.
допускают более простое решение по сравнению с решением систем уравнений (9.1), (9.2). Следует отметить, что данный метод обобщается на случай произвольного числа уравнений, содержащихся симметрических системах.
Кроме изложенного выше метода, существует еще много других, которые учитываются специфику заданной симметрической системы уравнений.