Методы решения функциональных уравнений

К числу наиболее сложных задач на вступительных конкурсных экзаменах по математике относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида

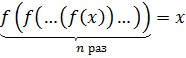(5.1)

или

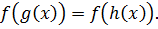(5.2)

где 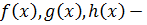некоторые функции и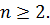

Методы решения функциональных уравнений (5.1), (5.2) основаны на использовании следующих теорем.

Теорема 5.1. Корни уравнения 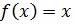являются корнями уравнения (5.1).

Доказательство. Пусть 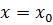– корень уравнения 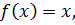т.е. 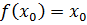. Тогда справедливы равенства

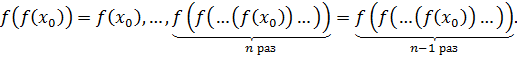
Отсюда следует, что

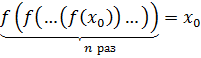
т.е. 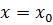является корнем уравнения (5.1).

Теорема 5.2. Если 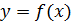- возрастающая функция на отрезке 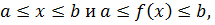то на данном отрезке уравнения (5.1) и 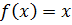равносильны.

Доказательство. Пусть 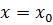является корнем уравнения (5.1), т.е.
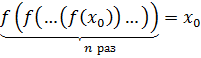. Предположим, что 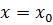не является корнем уравнения 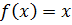, т.е. 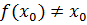. Не нарушая общности рассуждений, будем считать, что 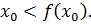Тогда в силу возрастания функции

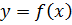справедливы неравенства

Так как 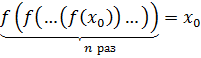, то из приведенных выше неравенств следует . Таким образом, получили ложное неравенство. А это означает, что .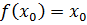

Отсюда и из теоремы 5.1 следует справедливость теоремы 5.2.

Следствие 1. Если функция 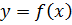возрастает для любого x, то уравнения (5.1) и f(x)=x равносильны.

Следствие 2. Если функция y=f(x) возрастает на своей области определения, то уравнения (5.1) и f(x)=x равносильны.

Более сложным является решение уравнения (5.1) в том случае, когда на некотором отрезке 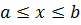функция 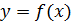является убывающей.

В данном случае имеют место аналогии теоремы 5.2 и двух следствий только при условии, что в уравнении (5.1) число n нечетное.

Теорема 5.3. Если y=f(x) – убывающая функция на отрезке 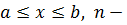нечетное и 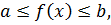то на данном отрезке уравнения (5.1) и f(x)=x равносильны.

Доказательство. Пусть 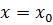является корнем уравнения (5.1), т.е.

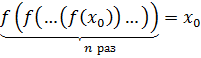
Предположим, что 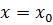не является корнем уравнения 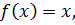т.е. 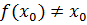. Не нарушая общности рассуждений, будем считать, что 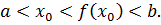Тогда в силу убывания функции 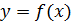на отрезке 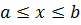получаем неравенства 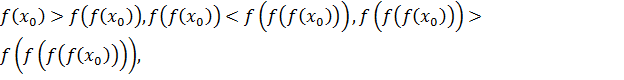и т.д.

Так как 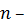нечетное, то .

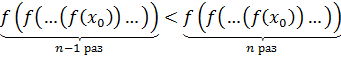Поскольку 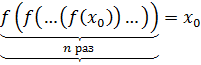, то из последнего неравенства получаем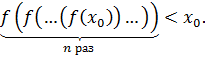

Так как 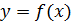– убывающая функция, то 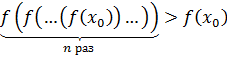, т.е. 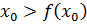. Получили противоречие тому, что по предположению 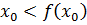. Следовательно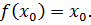

Отсюда, с учетом теоремы 5.1, следует справедливость теоремы 5.3.

Следствие 3. Если функция y=f(x) убывает для любого x и n – нечетное, то уравнения (5.1) и f(x)=x равносильны.

Следствие 4. Если функция y=f(x) убывает на своей области определения и n – нечетное, то уравнения (5.1) и f(x)=x равносильны.

Так как в рассмотренных выше случаях функция 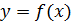является убывающей, то уравнение 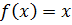может иметь только один корень. Поскольку уравнение (5.1) с убывающей функцией 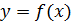и нечетным n равносильно уравнению 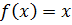, то уравнение (5.1) также имеет более одного корня.

Если в уравнении (5.1) 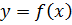- убывающая функция, а n – четное, то в общем случае уравнения (5.1) и 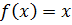не являются равносильными. Например, уравнение 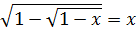имеет три корня и только третий корень удовлетворяет уравнению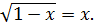

В данном случае для поиска корней уравнения (5.1) необходимо проводить дополнительные исследования.

Теорема 5.4. Если 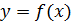– возрастающая (или убывающая) функция на области допустимых значений уравнения (5.2), то уравнения (5.2) и равносильны.

Доказательство. 1) Пусть - корень уравнения (5.2), т.е. 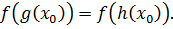Предположим, что 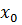не является корнем уравнения 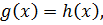т.е. 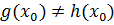. Не нарушая общности рассуждений, будем считать, что 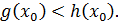Отсюда в зависимости от того, какой является функция y=f(x) на области допустимых значений уравнения (5.2) возрастающей или убывающей, получаем неравенство 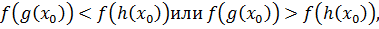соответственно. В каждом из двух случаем имеем ложное неравенство. Значит,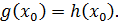

2) Пусть - корень уравнения 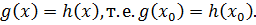Отсюда следует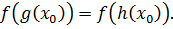

Следствие 5. Если 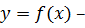возрастающая (или убывающая) функция на области значений 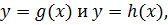то уравнения (5.2) и равносильны.

Также следует отметить, что при решении функционального уравнения (5.2) необходимо внимательно рассматривать случай, когда функция 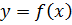является четной.

Теорема 5.5. Если четная функция 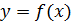определена на отрезке 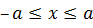и возрастает (или убывает) при 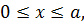то на данном отрезке уравнение (5.2) равносильно совокупности уравнений и 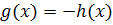при условии, что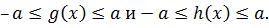

Доказательство проводится по аналогии с доказательством предыдущей теоремы. При этом используется четность функции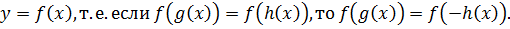

Анализ функции 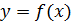на монотонность удобно осуществлять с помощью производной: если функция 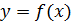дифференцируема на отрезке 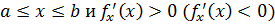, то функция 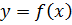является возрастающей (убывающей) на данном отрезке.