
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы, основанные на монотонности функций
|
|
При решении уравнений типа 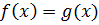 в ряде случаев весьма эффективным является метод, который использует монотонность функций
в ряде случаев весьма эффективным является метод, который использует монотонность функций 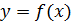 и
и 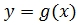 . Если функция
. Если функция 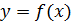 непрерывна и возрастает (убывает) на отрезке
непрерывна и возрастает (убывает) на отрезке 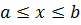 , а функция
, а функция 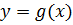 непрерывна и убывает (возрастает) на этом же отрезке, то уравнение
непрерывна и убывает (возрастает) на этом же отрезке, то уравнение 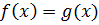 на отрезке
на отрезке 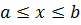 может иметь не более одного корня.
может иметь не более одного корня.
Напомним, что функция 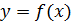 называется возрастающей (или убывающей) на отрезке
называется возрастающей (или убывающей) на отрезке 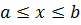 , если для любых
, если для любых 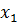 ,
, 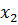 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 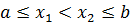 , выполняется неравенство
, выполняется неравенство 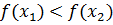 (соответственно,
(соответственно, 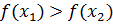 ). Если функция
). Если функция 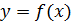 является на отрезке
является на отрезке 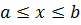 возрастающей или убывающей, то она называется монотонной на этом отрезке.
возрастающей или убывающей, то она называется монотонной на этом отрезке.
В этой связи при решении уравнения 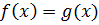 необходимо иследовать функции
необходимо иследовать функции 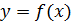 и
и 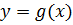 на монотонность, и если одна из этих функций на отрезке
на монотонность, и если одна из этих функций на отрезке 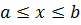 убывает, а другая функция – возрастает, то необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Если, например, функция
убывает, а другая функция – возрастает, то необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Если, например, функция 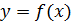 возрастает, а
возрастает, а 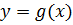 убывает для
убывает для 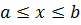 и при этом
и при этом 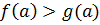 , то корней уравнения
, то корней уравнения 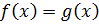 среди
среди 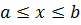 нет. Особенно такой метод эффективен в том случае, когда обе части уравнения
нет. Особенно такой метод эффективен в том случае, когда обе части уравнения 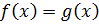 представляют собой весьма «неудобные» для совместного исследования функции.
представляют собой весьма «неудобные» для совместного исследования функции.
Кроме того, если функция 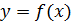 является монотонной на отрезке
является монотонной на отрезке 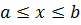 и уравнение
и уравнение 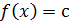 (где с – некоторая константа) имеет на этом отрезке корень, то этот корень единственный.
(где с – некоторая константа) имеет на этом отрезке корень, то этот корень единственный.