Рух частинок в кулонівському полі. Формула Резерфорда.

Закон Кулона для взаємодії двох точкових електричних зарядів, як відомо, виражається формулою

=k , де k=9*109Н*м²/Кл²

Ядра атомів, в яких зосереджена майже вся маса атома, заряджені позитивно. Величина заряду ядра атома рівна Ze, де Z - атомний номер елементу, е-модуль елементарного електричного заряду (заряду електрона). Дослідження будови атома проводиться шляхом зондування його пучком швидко рухомих заряджених частинок. При взаємодії частинок з ядром траєкторія останніх скривлюється, відбувається явище розсіяння частинок. Дослідами такого роду англійський фізик Резерфорд в 1911 р. встановив ядерну модель будови атома.

Розглянемо завдання про визначення траєкторії а-частіци, рухомою в полі ядра атома. У цьому завданні виходять формули Резерфорда для розсіяння α -частіц, що є ядрами гелію і що мають заряд 2е. Масу α -частіци позначимо m. Ядро розсіюючого атома має заряд Ze. Його масу вважаємо великою і рухом ядра нехтуємо. Потенційна енергія α -частіци

в полі ядра буде U =2kZe²\r, і за будь-яких початкових умов повна механічна енергія α -частіци позитивна, тобто Е > 0. Траєкторією руху в даному випадку є гіпербола, фокус якої співпадає з положенням розсіюючого ядра.

На малюнку 28.1 зображена траєкторія руху α -частіци і показані її елементи. АС - асимптота гіперболи, співпадаюча з напрямом початковій швидкості α -частіци, DB - друга асимптота, що визначає напрям швидкості α -частіци після розсіяння. Розсіююче ядро знаходиться в правому фокусі F₁. Кут 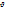між асимптотами - кут розсіяння, а і b - дійсна і уявна піввісь гіперболи - відстань від центру до фокусу гіперболи.

Відстань від розсіюючого центру до асимптоти F¹С=b є найменша відстань, на яке а-частіца пролетіла б від ядра за відсутності відштовхування. Ця відстань називається прицільною відстанню. Фактично найменша відстань, на якій частинка пролітає від ядра, є відстань від вершини гіперболи Е до фокусу F₁. Цю відстань позначимо через q, а через - кут між асимптотою і дійсною віссю гіперболи F₁F₂

Встановимо зв'язок між параметрами системи α -частіца - ядро і кутом відстані 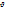. У результаті кут розсіяння повинен бути виражений через масу і швидкість частинки, її заряд і заряд ядра, прицільну відстань b, що характеризує взаємне положення ядра і налітаючої частинки.

Після не складних обрахунків ми отримаємо резельтат:

b= ctg , (28.1)що дає відповідь на поставлену задачу.

Але у випадку мікрочастинок прослідкувати за рухом окремих мікрочастинокв усіз деталях неможливо, тому співвідношення (28.1)безпосередньо не застосовується.

53. Меха́ ніка суці́ льних середо́ вищ — розділ механіки, присвячений вивченню руху і рівноваги газів, рідин, плазми і деформівних твердих тіл.

Вхідними у механіці суцільних середовищ при вивченні будь-якого середовища є:

1) рівняння руху або рівноваги середовища, які отримуються як наслідок основних законів механіки;

2) рівняння неперервності (суцільності) середовища, які є наслідком закону збереження маси;

3) рівняння збереження енергії;

4) рівняння стану або реологічне рівняння, яке встановлює для кожного конкретного середовища вид залежності між напруженнями і деформаціями або швидкостями деформації середовища, а також залежності характеристик від температури або інших фізико-хімічних параметрів.

Крім звичайних матеріальних тіл, подібних воді, повітрю чи металу, в механіці суцільних середовищ розглядаються також особливі середовища - поля: електромагнітне поле, гравітаційне поле та ін.

Рух суцільного середовища в просторі, на відміну від інших механічних систем, описується не координатами і швидкостями окремих частинок, а скалярним полем густини і векторним полем швидкостей. Залежно від завдань, до цих полів можуть додаватися поля інших фізичних величин (концентрація, температура, поляризація тощо). Якщо серед характеристик середовища зустрічаються тензорні величини, відповідні рівняння для суцільного середовища записують у тензорній формі.