Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тензор напружень
|
|
Те́ нзор механі́ чних напру́ жень або просто тензор напружень — тензор другого рангу, яким описуються сили, що виникають в твердому тілі при деформації.
Позначається здебільшого грецькою літерою σ, має розмірність тиску, тобто вимірюється в Паскалях.
Тензор механічних напружень визначається таким чином, щоб
 , де
, де  вектор сили, яка діє на одиницю об'єму речовини.
вектор сили, яка діє на одиницю об'єму речовини.
Тензор механічних напружень симетричний відносно 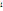 та
та 
Напруження стиску-розтягу та зсуву.
Тензор механічних напружень

Діагональні елементи матриці позначаються σ і назвиваються напруженнями стиску-розтягу, а недіагональні елементи позначаються τ і називаються напруженнями зсуву.
Рівняння рівноваги
У стані механічної рівноваги прикладена зовні сила діє лише на поверхню тіла. Всередині тіла кожен об'єм діє на сусідній з такою ж силою, що й сусідній діє на нього самого (третій закон Ньютона). В такому випадку справедливе рівняння рівноваги, що визначає деформацію тіла:
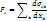
У випадку, коли на тіло діють так звані об'ємні сили, наприклад сили тяжіння, рівняння рівноваги набирає вигляду:

де ρ — густина речовини, а gi — компоненти об'ємних сил в розрахунку на одиницю об'єму.
Ці рівняння потрібно розв'язувати разом із граничними умовами.
Наприклад, якщо розтягувати довгий однорідний стрижень перерізом S, прикладаючи до його кінця силу F, то тензор механічних напружень матиме лише одну відмінну від нуля компоненту σ xx (вважаємо, що вісь x направлена вздовж стержня). Із граничних умов находимо 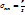
Тензор деформації
Те́ нзор деформа́ ції — математичний об'єкт, тензор, який характеризує зміщення кожної точки тіла при деформації.
Тензор деформації визначається, як 
де 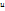 — вектор, який описує зміщення точки тіла.
— вектор, який описує зміщення точки тіла.
Тензор деформації симетричний, тобто  .
.
За допомогою тензора деформації описують малі пружні деформації тіла. При великих деформаціях, коли починає проявлятися незворотна пластичність або тіло рветься, застосування тензора деформації обмежене.
Діагональні елементи тензора деформації описують лінійні деформації розтягу чи стиску, недіагональні — деформацію зсуву.
В сферичній системі координат
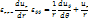
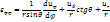



56. Основи гідродинаміки заклали в середині XVIII ст. Леонард Ейлер і Даніель Бернуллі. При вивченні певної задачі гідродинаміки використовують основні закони й методи механіки і, враховуючи загальні властивості рідин, дістають розв'язки, що дають змогу визначити швидкість, тиск або дотичні напруження зсуву в будь-якій точці простору, заповненого рідиною. Це дає змогу обчислити, зокрема, і зусилля, що виникають при взаємодії між рідиною й твердим тілом.
Експериментальна Гідродинаміка базується на теорії подібності і розмірностей.
Закони Гідродинаміки використовують при проектуванні суден, літаків, турбін, трубопроводів, гідротехнічних споруд, при дослідженні морських течій, фільтрації підземних вод і нафти в родовищах.
Ідеальна рідина — рідина, для якої неістотні процеси теплопровідності і в'язкості.
Рух ідеальної рідини описується рівняннями Ейлера і відбувається адіабатично, тобто ентропія будь-якого елементу рідини залишається незмінною.
Вздовж струменів рідини виконується закон Коші-Бернуллі:
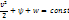
де 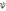 — потенціал зовнішніх сил, а
— потенціал зовнішніх сил, а 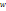 — ентальпія одиниці маси рідини. Стала, яка входить в закон Коші-Бернулі, є сталою лише для даного струменя і може мати різні значення в різних точках рідини.
— ентальпія одиниці маси рідини. Стала, яка входить в закон Коші-Бернулі, є сталою лише для даного струменя і може мати різні значення в різних точках рідини.
Ідеальна рідина називається потенціальною, якщо для неї виконується умова:  , де
, де  поле швидкостей.
поле швидкостей.
Потенціальну ідеальну рідину можна описати потенціалом:  .
.
57. Рівняння Нав'є́ — Сто́ кса — система диференціальних рівнянь у частинних похідних, що описує рух і теплопередачу в'язкої н'ютонової рідини. Рівняння Нав'є-Стокса являються одними з найважливіших у гідродинаміці й застосовуються в математичному моделюванні багатьох природних явищ і технічних задач. Названі по імені французького фізика Луї Нав'є й британського математика Джорджа Стокса.
Система складається з двох рівнянь:
-рівняння руху,
-рівняння нерозривності.
В векторному виді для нестисливої рідини вони записуються в такий спосіб:

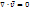
де  — оператор Гамільтона, Δ — оператор Лапласа, t — час, ν — коефіцієнт кінематичної в'язкості, ρ — щільність, p — тиск,
— оператор Гамільтона, Δ — оператор Лапласа, t — час, ν — коефіцієнт кінематичної в'язкості, ρ — щільність, p — тиск, 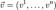 — векторне поле швидкостей,
— векторне поле швидкостей,  — векторне поле масових сил. Невідомі p і V являються функціями часу t і координати
— векторне поле масових сил. Невідомі p і V являються функціями часу t і координати 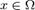 , де
, де  , n = 2, 3 — плоска або тривимірна область, у якій рухається рідина. Звичайно в систему рівнянь Нав'є́ — Стокса додають крайові й початкові умови, наприклад
, n = 2, 3 — плоска або тривимірна область, у якій рухається рідина. Звичайно в систему рівнянь Нав'є́ — Стокса додають крайові й початкові умови, наприклад