
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие дифференциала функции
|
|
Пусть функция  имеет в точке
имеет в точке  отличную от нуля производную
отличную от нуля производную  ≠
≠  . Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать 
 где
где  при
при  .
.
Таким образом, приращение функции  представляет собой сумму двух слагаемых
представляет собой сумму двух слагаемых  являющихся бесконечно малыми при
являющихся бесконечно малыми при  При этом первое слагаемое есть бесконечно малая функция одного порядка с
При этом первое слагаемое есть бесконечно малая функция одного порядка с  так как
так как  ≠
≠  , а второе слагаемое есть бесконечно малая функция более высокого порядка,
, а второе слагаемое есть бесконечно малая функция более высокого порядка, 

 .
.
Поэтому первое слагаемое  называемых главной частью приращения функции
называемых главной частью приращения функции 
Дифференциальном функции  в точке
в точке 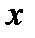 называется главная часть ее приращения, разная произведению производной функции на приращение аргумента, и обозначается
называется главная часть ее приращения, разная произведению производной функции на приращение аргумента, и обозначается 

Дифференциал  называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной  т.е. дифференциал функции
т.е. дифференциал функции 
Так как  то, согласно формуле, имеем
то, согласно формуле, имеем  т.е. дифференциал независимой переменной равен приращению этой переменной:
т.е. дифференциал независимой переменной равен приращению этой переменной: 
Поэтому формулу можно записать так:

|
Иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы следует равенство  Теперь обозначение производной
Теперь обозначение производной  можно рассматривать как отношение дифференциалов
можно рассматривать как отношение дифференциалов  и
и 
Пример 1. Найти дифференциал функции

Решение: По формуле  находим
находим

Пример 2. Найти дифференциал функции

Вычислить  при
при 
Решение: 
Подставив  и
и  получим
получим
