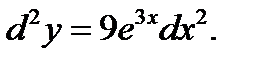Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциалы высших порядков
|
|
Пусть  дифференцируемая функция, а ее аргумент
дифференцируемая функция, а ее аргумент  независимая переменная. Тогда ее первый дифференциал
независимая переменная. Тогда ее первый дифференциал 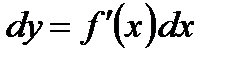 есть также функция
есть также функция 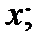 можно найти дифференциал этой функции.
можно найти дифференциал этой функции.
Дифференциал от дифференциала функции  называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается
называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается  или
или 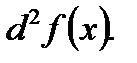
И так, по определению 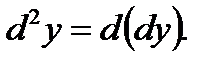 Найдем выражение второго дифференциала функции
Найдем выражение второго дифференциала функции 
Так как  не зависит от
не зависит от  то при дифференцировании считаем
то при дифференцировании считаем  постоянным:
постоянным:

т.е.

Здесь 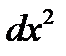 обозначает
обозначает 
Аналогично определяется и находится дифференциал третьего порядка:

И, вообще, дифференциал  -го порядка есть дифференциал от дифференциала
-го порядка есть дифференциал от дифференциала  -го порядка:
-го порядка: 
Отсюда находим, что 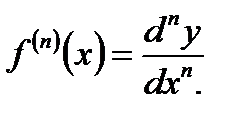 В частности, при
В частности, при 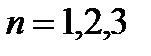 соответственно получаем:
соответственно получаем: 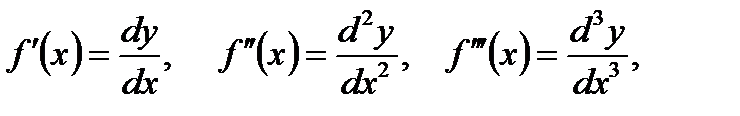
т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведенные выше формулы справедливы только, если  - независимая переменная. Если же функцию
- независимая переменная. Если же функцию 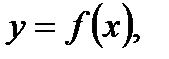 где
где  - функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
- функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
Используя формулу дифференциала произведения 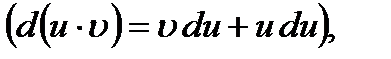 получаем:
получаем:
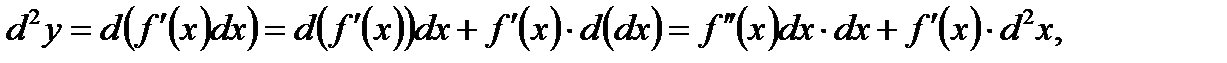
т.е.

Сравнивая формулы и убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое 
Ясно, что если  - независимая переменная, то
- независимая переменная, то

и формулу переходит в формулу.
Пример. Найти 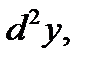 если
если  и
и 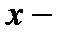 независимая переменная.
независимая переменная.
Решение: Так как  то по формуле имеем
то по формуле имеем