Метод исключения Гаусса и LU разложение.

Наиболее распространенным прямым методом решения систем линейных алгебраических уравнений является метод исключения Гаусса. Доказано, что система уравнений вида

(1.1)

с заполненной матрицей не может быть решена за число шагов меньшее, чем то, которое требуется для реализации метода Гаусса.

Гауссовское исключение существует во многих вариантах, которые алгебраически эквивалентны, но отличаются друг от друга порядком исключения элементов, способами предупреждения больших погрешностей. Описание различных вариантов метода приведено в работах [1-4].

Алгебраической основой метода исключения является представление матрицы А в виде произведения А=LU, где L={ } -нижняя треугольная матрица, = =…= =1; U={ u } -верхняя треугольная матрица. Представление А=LU называется LU разложением матрицы А.

Докажем эквивалентность метода Гаусса определению LU разложения матрицы А.

Рассмотрим обыкновенное Гауссовское исключение без перестановок. Допустим, чтоа 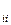0, .

Первый шаг метода состоит в исключении неизвестной 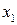из всех уравнений системы за исключением первого. Обозначим систему уравнений, полученную после первого шага через А . Пусть матрица А = . Используяправило умножения матриц нетрудно убедиться в том, что А =М А, =М , где М - нижняя треугольная матрица,

М = .

Здесь

, , (1.2)

а коэффициенты матрицы А вычисляются по формулам:

. (1.3)

На втором шаге метода система уравнений А приводится к системе А , в которой переменная исключена из всех уравнений, кроме первых двух. В матричных обозначениях это соответствует умножению А и на нижнюю треугольную матрицу М ,

М = ,

где

. (1.2)

Таким образом, А =М А =М М А, = М = М М .

Коэффициенты матрицы А вычисляются так

. (1.3)

Аналогичные соотношения связывают левые и правые части систем уравнений, полученных на -ом и ( -1)-ом шагах ()

А =М А =М М …М А, =М = М М …М , (1.4)

здесь М - нижняя треугольная матрица с ненулевыми поддиагональными элементами в -ом столбце.

На последнем ()-ом приходим к системе уравнений А , где А - верхняя треугольная матрица, коэффициенты которой вычисляются по формулам

(1.2)

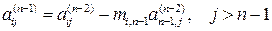(1.3)

Обозначим А =U, тогда

Из формулы (1.4) следует, что имеет место матричное равенство М М …М А=U или А=LU, где L=М М …М . Матрицы L и U имеют, соответственно, вид нижней и верхней треугольных матриц:

L= = , U= .

Коэффициенты матрицы L={ }, = 0, при ; = 1, при ; при вычисляются по формулам (1.2), а , при , определяются по формулам (1.3).

Итак, если на каждом шаге , то можно получить такие верхнюю U и нижнюю L треугольные матрицы, что А=LU, причем

.