
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод наименьших квадратов.
|
|
Пусть функция задана на некотором дискретном или непрерывном множестве А. Выберем систему линейно независимых функций  , заданных на множестве. Рассмотрим задачу приближения функции
, заданных на множестве. Рассмотрим задачу приближения функции  на множестве А многочленом
на множестве А многочленом  вида
вида
 .
.
При фиксированной системе функций  многочлен
многочлен  однозначно определяется коэффициентами
однозначно определяется коэффициентами  , т.е.
, т.е.  . Многочлен
. Многочлен  называется многочленом наилучшего среднеквадратичного приближения функции
называется многочленом наилучшего среднеквадратичного приближения функции  на множестве А, если выполняется соотношение
на множестве А, если выполняется соотношение
 .
.
Здесь
 .
.
Можно показать, что коэффициенты  , минимизирующие квадрат расстояния
, минимизирующие квадрат расстояния  , должны удовлетворять системе линейных уравнений
, должны удовлетворять системе линейных уравнений
 , (4.6)
, (4.6)
где
 .
.
Систему уравнений (4.6) называют нормальной системой. Благодаря предположению о линейной независимости функций  решение системы (4.6) всегда существует и единственно.
решение системы (4.6) всегда существует и единственно.
Приближение функций алгебраическими многочленами. Часто для среднеквадратичных приближений используют системы алгебраических многочленов. Система степенных функций является простейшей и имеет вид
 . (4.7)
. (4.7)
Такая система линейно независима в пространстве  непрерывных на интервале
непрерывных на интервале  функций. В пространстве
функций. В пространстве 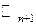 функций, заданных таблично на множестве точек
функций, заданных таблично на множестве точек  , система (4.7) линейно независима при
, система (4.7) линейно независима при  и линейно зависима в противном случае.
и линейно зависима в противном случае.
Пример 6. Для функции  построить многочлен наилучшего среднеквадратичного приближения по системе степенных функций (4.7) для двух значений
построить многочлен наилучшего среднеквадратичного приближения по системе степенных функций (4.7) для двух значений  , равных 2 и 3. Вычислить значение квадрата расстояния от
, равных 2 и 3. Вычислить значение квадрата расстояния от  до приближаемой функции
до приближаемой функции  , т.е.
, т.е. 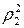 при
при  и
и  при
при  . Определить величину относительного уменьшения ошибки аппроксимации
. Определить величину относительного уменьшения ошибки аппроксимации  .
.
Решение. Найдем многочлен наилучшего среднеквадратичного приближения функции  . Для расчета коэффициентов нормальной системы уравнений необходимо воспользоваться справочниками, содержащими таблицы интегралов от степенных и тригонометрических функций. Напомним, что
. Для расчета коэффициентов нормальной системы уравнений необходимо воспользоваться справочниками, содержащими таблицы интегралов от степенных и тригонометрических функций. Напомним, что
 .
.
1.  . В наших обозначениях
. В наших обозначениях  . Коэффициенты нормальной системы уравнений
. Коэффициенты нормальной системы уравнений
 .
.
Следовательно, нормальная система уравнений относительно неизвестных 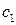 и
и  имеет вид:
имеет вид:
 .
.
Решая систему, получим
 .
.
Многочлен наилучшего приближения

 .
.
2.  . В данном случае
. В данном случае 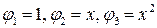 . Нормальная система уравнений
. Нормальная система уравнений
 .
.
Решение системы
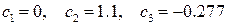 .
.
Многочлен наилучшего приближения
 .
.
Следует отметить, что вычисления коэффициентов многочлена необходимо проводить с точностью до третьего знака после запятой.
Вычислим квадрат расстояния от приближаемой функции  до многочлена наилучшего приближения
до многочлена наилучшего приближения
 .
.
Относительная ошибка аппроксимации
 .
.
Видно, что ошибка аппроксимации функции  многочленом
многочленом  почти в три раза меньше, чем при аппроксимации многочленом
почти в три раза меньше, чем при аппроксимации многочленом  .
.
Варианты заданий для выполнения контрольной работы.
Контрольная работа состоит из 5 заданий.
Задание 1. Решить систему линейных уравнений А  методом LU- разложений.
методом LU- разложений.

| 
|

| 
|

| 
|

| 
|
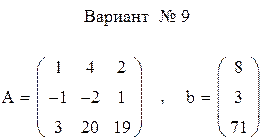
| 
|
Задание 2. Оценить погрешность решения системы уравнений  ( см. задание 1), если погрешность задания вектора
( см. задание 1), если погрешность задания вектора  равна 0.01.
равна 0.01.
Задание 3. Решить систему линейных уравнений

методом итераций с погрешностью, не превышающей  =0.01.
=0.01.
| Номер варианта | 
| 
|
Задание 4. Построить квадратичный интерполяционный многочлен Лагранжа для функции  на отрезке
на отрезке  . Найти оценку погрешности интерполяции на всем отрезке.
. Найти оценку погрешности интерполяции на всем отрезке.
| Номер варианта | 
| 
|

| 
| |
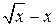
| 
| |

| 
| |
 
| 
| |
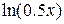
| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
|
Задание 5. Приближаемая функция  задана на отрезке
задана на отрезке  .Требуется построить многочлен наилучшего среднеквадратичного приближения по системе степенных функций
.Требуется построить многочлен наилучшего среднеквадратичного приближения по системе степенных функций  для двух значений
для двух значений  , равных 2 и 3. Вычислить значение квадрата расстояния от
, равных 2 и 3. Вычислить значение квадрата расстояния от  до приближаемой функции
до приближаемой функции  , т.е.
, т.е. 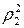 при
при  и
и  при
при  . Определить величину относительного уменьшения ошибки аппроксимации
. Определить величину относительного уменьшения ошибки аппроксимации  .
.
| Номер варианта | 
| 
|
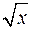
| 
| |
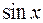
| 
| |
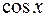
| 
| |
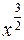
| 
| |

| 
| |
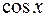
| 
| |
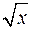
| 
| |
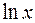
| 
| |
| 
| |

| 
|