Решение системы алгебраических уравнений методом LU-разложений.

С помощью изложенной выше схемы уравнение

А

представим в виде:

А LU .

Решение последнего уравнения эквивалентно решению системы уравнений:

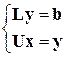(1.5)

с треугольными матрицами L и U.

Вначале найдем решение системы L с нижнетреугольной матрицей L, в результате найдем вектор 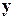. Далее найдем решение системы U 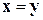с верхнетреугольной матрицей U, т.е. искомый вектор :

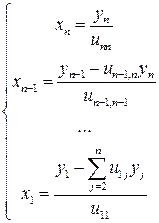, (1.6).

В методе исключения с перестановками прямой ход также равносилен LU- разложению, но не самой матрицы А, а полученной из нее в результате перестановок.

Пример 1. Решить систему А , где

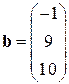А= , (1.7)

методом LU- разложений.

Решение. На первом этапе построим LU- разложение матрицы А.

Шаг 1: по формулам (1.2) находим . Элементы матрицы А вычислим по формулам (1.3) :

А = .

Шаг 2: по формуле (1.2) вычисляем, что коэффициент . Элементы матрицы А получим используя формулы (1.3) :

А = .

Итак, построены матрица U=М М А=А и матрица L

. (1.8)

Этап 2. С помощью формул (1.6) найдем решение системы (1.5): 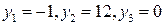, компоненты искомого вектора равны: ,

.