Погрешности решения систем линейных алгебраических уравнений.

Погрешность результата решения системы (1.1) определяется следующими причинами:

1. Неточность информации о решаемой задаче. Ошибки в начальных данных определяют ту часть погрешности, которая не зависит от математической стороны решения задачи и называется неустранимой погрешностью.

2. Погрешность аппроксимации или погрешность метода. Пари решении задач линейной алгебры итерационными методами неизбежно приходится иметь дело только с конечным числом операций, что позволяет подходить к решению с определенной точностью.

3. Погрешность округлений. Влияние этих ошибок приводит к тому, что в действительности вместо системы (1.1) решается система вида

, (2.1)

где - матрица погрешностей элементов , - вектор погрешностей компонент .

Обозначим через погрешность решения системы (1.1) и оценим влияние ошибок в и на величину .

Поскольку , то удовлетворяет уравнению

откуда следует, что

.

Умножив последнее равенство слева на и, пренебрегая слагаемыми второго порядка малости, получим

.

Следовательно,

.

Это неравенство приводит к следующему неравенству для относительной ошибки :

.

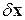
Поскольку , то

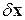
, (2.2)

здесь слагаемые в скобках представляют собой относительные погрешности = элементов матрицы и вектора .

Из неравенства (2.2) следует, что мерой чувствительности результата решения системы (1.1) к погрешностям в исходных данных может служить число , называемое числом обусловленности матрицы , .

Если погрешности в исходных данных приводят к значительным погрешностям в решении ( имеет большое значение), то система называется плохо обусловленной.

Пример 2. Оценить погрешность решения системы линейных уравнений , где матрица и вектор заданы выражениями (1.7), если погрешность задания правой части системы =0.01.

Решение. Погрешность решения системы линейных уравнений определяется числом обусловленности матрицы системы и, в данном случае ( =0),

.

Относительная погрешность вектора равна

.

Для получения числа обусловленности необходимо вычислить нормы матриц и . Норма матрицы

.

Норму обратной матрицы получим с помощью LU- разложения матрицы А

.

Обратим матрицы и , используя выражение (1.8)

.

Отсюда для матрицы получаем выражение

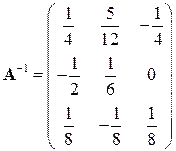
из которого следует, что .

Число обусловленности .

Итак, погрешность решения можно оценить следующим образом:

.