
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Численные методы приближения функций.
|
|
Приближением функции называется процедура замены по определенному правилу функции  близкой к ней в том или ином смысле функцией
близкой к ней в том или ином смысле функцией  из некоторого фиксированного множества. В качестве приближающего множества частот берут подпространство алгебраических или тригонометрических многочленов (полиномов). Более гибкий и мощный аппарат приближения получают, рассматривая обобщенные полиномы
из некоторого фиксированного множества. В качестве приближающего множества частот берут подпространство алгебраических или тригонометрических многочленов (полиномов). Более гибкий и мощный аппарат приближения получают, рассматривая обобщенные полиномы
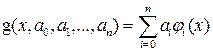 ,
,
где  – некоторая система линейно независимых функций, выбираемая с учетом конкретных условий задачи и требований, предъявляемых к функции
– некоторая система линейно независимых функций, выбираемая с учетом конкретных условий задачи и требований, предъявляемых к функции  . В дальнейшем будем считать, что функция
. В дальнейшем будем считать, что функция  – полином такого вида.
– полином такого вида.
Мерой погрешности приближения является, как правило, расстояние  между приближаемой и приближающей функциями. Наиболее часто погрешность приближения на интервале
между приближаемой и приближающей функциями. Наиболее часто погрешность приближения на интервале  оценивается в равномерной
оценивается в равномерной

и среднеквадратичной

метриках, где  – интервал, на котором строится приближение.
– интервал, на котором строится приближение.
Рассмотрим две постановки задачи приближения.
1. Пусть в отдельных точках  интервала
интервала  заданы значения функции
заданы значения функции  ; требуется восстановить ее значение для других
; требуется восстановить ее значение для других  .
.
Если параметры  определяются из условий совпадения значений приближаемой и приближающей функций в точках
определяются из условий совпадения значений приближаемой и приближающей функций в точках 
 ,
,
то такой способ приближения называют интерполяцией, а точки  – узлами интерполяции. (Задачей экстраполяции называют задачу вычисления функции
– узлами интерполяции. (Задачей экстраполяции называют задачу вычисления функции  в некоторой точке
в некоторой точке  , находящейся вне интервала
, находящейся вне интервала  ).
).
Предположим, что алгоритм построения приближающей функции не требует выполнения последнего условия, и значения функции вычисляются в произвольных точках, тогда говорят об аппроксимации функции.
2. Пусть функция  задана таблично по результатам измерений, т.е. значения функции
задана таблично по результатам измерений, т.е. значения функции  , вычисленные в точках
, вычисленные в точках  ,
,  , содержат ошибки
, содержат ошибки  . Построение приближающего полинома интерполяционным методом с использованием условий совпадения значений приближаемой и приближающей функций в узлах привело бы к повторению имеющихся ошибок.
. Построение приближающего полинома интерполяционным методом с использованием условий совпадения значений приближаемой и приближающей функций в узлах привело бы к повторению имеющихся ошибок.
Практика показала, что полином  , минимизирующий погрешность приближения в среднеквадратичной метрике, значительно лучше представляет функцию
, минимизирующий погрешность приближения в среднеквадратичной метрике, значительно лучше представляет функцию  . Таким образом, аппроксимирующий полином
. Таким образом, аппроксимирующий полином  строится из условия
строится из условия
 .
.
Процедура таких построений носит название метода наименьших квадратов.