Свойства определителя квадратной матрицы. Вычисление определителя приведением к треугольному виду

Свойства определителей.

1) При транспортировании матрицы значение определителя не меняется, т.е. .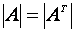

Замечание: это свойство означает, что всякое свойство определителя, связанное со строками, справедливо и для столбцов.

2) Если в определителе две строки (два столбца) пропорциональны, то он равен нулю. В частности, определитель равен нулю, если две строки (два столбца) совпадают или одна строка (столбец) нулевая.

3) Если поменять местами две строки (столбца), то определитель изменит свой знак на обратный.

4) Если строку (столбец) умножить на одно и то же число, то определитель умножится на это число.

5) Если к строке (столбцу) прибавить другую строку (столбец), умноженную на число, то определитель не изменится.

6) Определитель, в котором строка представлена как сумма строк, равен сумме соответствующих определителей.

7) Определитель не меняется, если к одной строке прибавить другую, умноженную на число.

8) При элементарных преобразованиях матрицы, определитель отличный от 0 останется отличным от 0, а определитель, равный 0, останется равным 0.

Доказательство: поскольку элементарные преобразования обратимы: а) можно строки обратно поменять местами; б) можно прибавить ту же строку, умноженную на противоположное число; в) можно умножить на обратное число.

Утверждение достаточно доказать только относительно определителя, отличного от 0.

9) Определитель произведения матриц равен произведению определителей. |A_nxn*B_nxn|=|A|*|B|

Вычисление определителя приведением к треугольному виду.

Треугольная матрица — матрица, в которой все элементы ниже главной диагонали равны нулю.

Дана матрица размером 3х3;

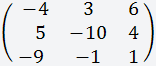
1.1 Для простоты решения (что бы не было дробей) необходимо, что бы первый элемент первой строки был равен единице, поэтому ко второй строке добавляем первую строку и меняем их местами;

1.2 Меняем местами первую строку со второй;

2. Следующим шагом нужно обнулить первые элементы второй и третей строки (-4 и -9). Для этого из второй строки вычитаем первую строку, умноженную на первый элемент второй строки, т.е. на -4, тем самым обнулится первый элемент второй строки. Тоже самое проделываем с третей строкой, только умножаем первую строку на первый элемент третей строки (-9)

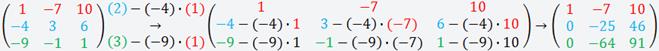
*Если обнуляемый элемент является отрицательным, тогда проще, к этой строке добавить первую строку умноженную на этот же элемент противоположного знака, т.е. (2) - (-4) × (1) = (2) + 4 × (1)

3. Для того что бы обнулить второй элемент третей строки (-64) и превести матрицу к треугольному виду, желательно второй элемент второй строки (-25) привести к 1-е, но это долго и сложно, поэтому с ним ни чего не делаем.

4. Далее обнуляем второй элемент третей строки, вычитая из неё вторую строку, умноженную на 64/25, что приведёт матрицу к треугольному виду.