
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Получение обратной матрицы с помощью присоединенной.
|
|
Предположим, что матрица A - неособенная и рассмотрим метод нахождения обратной матрицы, основанный на элементарных операциях над строками.
В данном контексте под элементарными преобразованиями понимается:
- Умножение строки на любое ненулевое число.
- Прибавление к одной строке любой другой, предварительно умноженной на любое число.
Алгоритм метода чрезвычайно прост по своей сути.
Сначала составляется расширенная матрица – присоединением к матрице A единичной матрицы E:

Затем с помощью элементарных операций над строками расширенная матрица (A | E) преобразуется к виду (E | B).
С формальной точки зрения такие преобразования могут быть реализованы умножением на матрицу A некоторой матрицы T, которая представляет собой произведение соответствующих элементарных матриц (матрицы перестановки, матрицы масштабирования, неунитарной матрицы):
TA = E.
Это уравнение означает, что матрица преобразования T представляет собой обратную матрицу для матрицы A:
T = A -1.
Тогда TE = A -1 и, следовательно,

ПРИМЕР: Методом элементарных преобразований найти обратную матрицу для матрицы: А=  .
.
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: 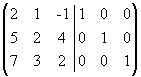 . С помощью элементарных
. С помощью элементарных
преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 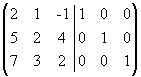 ~
~  . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:  . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй;  . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму:  . Умножим последний столбец на -1:
. Умножим последний столбец на -1:  . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
 .
.