
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная зависимость системы векторов. Критерий линейной зависимости.
|
|
Мы рассматриваем столбцы или строки одинаковой длины.
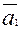 ,
, 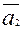 , …,
, …, 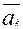
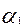
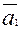 +
+ 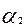
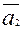 +…+
+…+ 
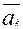 - такое выражение называется линейной комбинацией системы.
- такое выражение называется линейной комбинацией системы.
Система векторов наз-ся линейнозависимой, если существует такая её линейная комбинация, которая равна нулевому вектору, причем не все коэфф-ты этой комбинации равны нулю.
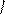 т.е.
т.е. 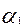
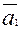 +
+ 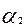
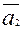 +…+
+…+ 
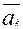 =
= 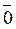
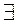
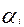 = 0
= 0
Теорема
Критерий линейной зависимости.
Система векторов линейнозависима тогда и только тогда, когда один из векторов системы линейно выражается через другие.
Док-во(для 4ех векторов)

 1)Пусть
1)Пусть 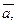
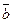 ,
, 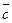 ,
, 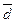 линейнозависимые
линейнозависимые 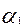
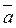 +
+ 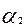
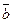 +
+ 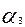
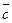 +
+ 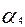
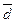 = 0
= 0
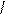
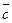 =-
=- 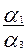
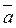 -
- 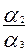
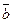 -
- 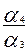
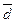 (при
(при 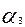
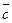 =0)
=0)
2)Пусть 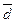 =
= 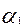
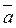 +
+ 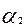
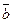 +
+ 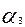
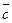
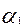
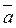 +
+ 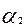
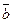 +
+ 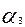
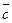 +(-1)
+(-1) 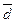 =
= 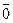
Св-ва линейн.зависимой системы:
1) Если система содержит нулевой вектрой.то она линейнозависима.
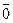 ,
, 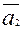 ,
, 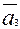 , …,
, …, 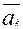
1* 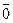 +0*
+0* 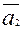 +0*
+0* 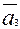 +…+0*
+…+0* 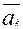 =
= 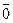
2) Если подсистема системы векторов является лин.зависимой, то и вся система явл-ся лин.зависимой.
Док-во.
Переименуем вектора так, что первые к векторов явл-ся лин.зависимыми.

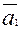 ,
, 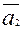 , …,
, …, 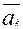 ,
, 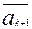 , …,
, …, 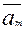
лин. завис.
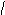
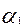
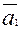 +…+
+…+ 
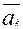 =0
=0 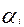 = 0
= 0
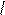
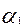
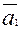 +
+ 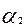
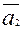 +…+
+…+ 
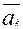 +0*
+0* 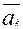 +…+0*
+…+0* 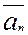 =0
=0 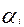 = 0
= 0