Ступенчатый вид и совместность систем линейных уравнений.

Теорема1.

Система совместна тогда и только тогда, когда в ступенчатом виде расширенной матрицы последняя ненулевая строка содержит отличные от нуля элементы не на последнем месте.

(0 0 …0 b = 0)

Соответственно уравнение имеет вид:

0*х₁+…+0*х_n = b = 0

х₁+2х₂-х₃+х₄=1

х₁-х₂+х₃-х₄=2

2х₁+4х₂-2х₃+2х₄=3

Определение.

Столбцы ступенчатой матрицы, отвечающие первым ненулевым элементам строк наз-сяведущими, а неизвестные, отвечающие этим столбцам наз-ся главными(базисными).

Остальные неизвестные наз-ся свободными.(их может и не быть)

Теорема2.

Совместная СЛУ является определенной тогда и только тогда, когда все неизвестные являются главными.

Док-во:

Действительно, в улучшенном ступенчатом виде получим тогда единичную матрицу и столбец свободных членов.

х₁=b₁ х₂=b₂ …. x_n=b_n

Если же есть свободные неизвестные, то как только они примут конкретные значения, сразу определяться значения главных неизвестных.

(но свободные неизвестные могут принимать какие угодно значения, а значит, если они имеются, то множество решений обязано быть даже бесконечным)

Теорема3.

Если в ступенчатом виде не все неизвестные главные (т.е. имеются свободные), то в этом случае система имеет бесконечное множество решений.

Пример.

х₁+2х₂ =2

х₁+х₂-х₃+х₄=4

2х₁+2х₂-2х₃+х₄=7

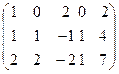
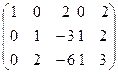
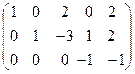
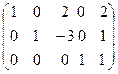
(Х₃ может быть каким угодно)

х₁=2-2х₃ х₃=t

х₂=1+3х₃

х₄=1

х₁=2-2 t ₃ x= t*

х₂=1+3 t ₃

х₄=1