
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейные действия над матрицами, восемь свойств этих действий.
|
|
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
Умножить матрицу А на матрицу В означает последовательно умножить строки А на столбцы В и получить новую матрицу.
Умножение i-ой строки на j-ый столбец дает элемент, который стоит на i-ой строке и на j-том столбце.
Свойства:
1) A+B=B+A
2) (A+B)+C=A+(B+C)
3) существует нулевая матрица  (тех же размеров, что и
(тех же размеров, что и  ):
):  ;
;
4) существует матрица  , противоположная матрице
, противоположная матрице 
5)  ;
;
6)  ;
;
7) 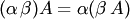 ;
;
8) 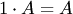
Умножение матриц, свойства умножения матриц. Транспонированная матрица.
Произведение матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
 |
Пусть даны матрица А размера [ п х т ] и матрица В размера [ т х р ].
Произведением двух матриц А и В, заданных в определённом порядке (А - первая, В - вторая), называется матрица С размера [ п х р ], элементы с ij которой определяются по следующему правилу: элемент i -й строки и j- го столбца матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j- го столбца матрицы В (рис.43), т.е.
c ij = ai1b1 j + ai2b2 j + … + aimbmj = 
i = 1, 2, …, n; j = 1, 2, …, p.
Произведение матриц А и В, взятых в указанном порядке, обозначается А·В или АВ.

|
 |
Произведением двух прямоугольных матриц является снова прямоугольная матрица, число строк которой равно числу строк первой матрицы, а число столбцов – числу столбцов второй матрицы. Из определения умножения матриц видно, что если возможно умножение матрицы А на матрицу В, то отсюда не следует возможность умножения матрицы В на матрицу А. Умножение матриц не обладает свойством перестановочности, поэтому если оба произведения АВ и ВА имеют смысл, то АВ может не совпадать с ВА. В том случае, когда оба произведения АВ и ВА определены и выполняется равенство АВ=ВА, матрицы А и В называют перестановочными.
Умножение матриц обладает следующими свойствами:
Свойство 1. А(ВС)=(АВ)С
Свойство 2. " lÎ Â (l(АВ)=(lА)В=А(lВ))
Свойство 3. С (А+В)=СА+СВ
Свойство 4. (А+В)С=АС+ВС
Свойство 5. (АВ)Т=ВТАТ , где А, В, С – матрицы, а l – число, а АТ это матрица, полученная из матрицы А в результате транспонирования.
Транспонировать матрицу означает поменять местами строки и столбцы.
