Теорема о том, что общее решение неоднородной системы линейных уравнений есть сумма частного решения неоднородной системы и общего решения однородной системы.

Теорема

Решение однородной, неоднородной системы обладает след-ми св-ми:

1). Разность решений неоднородной системы является решением однородной.

2).Сумма решений неоднородной и однородной систем является решением неоднородной.

Док-во.

АХ=В, АУ=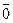

А(Х+У)=АХ+АУ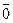=В+ =В

АX=В, АZ=B А(Х-Z)=АХ-АZ=B-B=

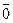
Следствие

Общий вид решений неоднородной системы может быть описан след.образом, в виде равенства двух множеств.

Хон=Хоо+Хчн

он-общее решение неоднор.системы, оо- общее решение однородн.системы, чн- частное решение неоднородн.системы(выбрано заранее)

1)Х правой части Х левой части (уже доказано)

2)Х левой части АХ=В, АХчн=В Х-Хчн=У(рещение системы 2)

Х=У+Хчн

Замечание

Тот вид, которго мы добивались для решения неоднородной системы соответствует этому св-ву.

Пример

Пусть главные неизвестные уже выражены через свободные.

Х1, Х3 – главные

Х2=S, Х4=T, Х5=U- свободные

Х1=2S-3T+U-7

X2=S

X3=T-2U+5

X4=T

X5=U

X=S +T +U +

Xoo Xчн