
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретичні відомості.
|
|
Зміст роботи.
І. Рівняння, системи рівнянь, нерівності та системи нерівностей, які містять знак абсолютної величини. Теоретичні відомості.
ІІ. Рівняння.
Завдання для самостійного розв’язання.
ІІІ. Нерівності.
Нерівності загального виду.
Нерівності виду або.
Нерівності виду.
Нерівність виду.
5. Нерівність виду 
Застосування заміни змінної в нерівностях.
Нерівності виду, що розв’язуються розкладанням лівої частини на
Множники.
Дробово – раціональні нерівності з невід’ємним знаменником.
Нерівності зі складним модулем.
Завдання для самостійного розв’язання.
IV. Рівняння і нерівності з параметрами, що містять знак абсолютної величини.
Завдання для самостійного розв’язання
V. Системи рівнянь що містять абсолютну величину і параметри.
Завдання для самостійного розв’язання.
VI. Використання властивостей модуля до розв’язування нестандартних завдань.
Завдання для самостійного розв’язання.
І.Рівняння, системи рівнянь, нерівності та
Системи нерівностей, які містять знак
Абсолютної величини.
Теоретичні відомості.
 Абсолютна величина (модуль) числа а позначається
Абсолютна величина (модуль) числа а позначається 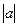 .
.
Означення 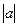 = a, a
= a, a 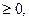
-а, а 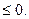
Властивості абсолютної величини числа:
1.  2.
2. 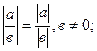
3.  4.
4. 
5. 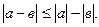
Часто при розв’язуванні рівнянь та нерівностей користуються наступними властивостями модуля:
6.  7.
7. 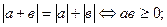
8. 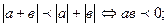 9.
9. 
10. 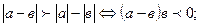 11.
11. 
Схеми розв’язання основних типів рівнянь з модулем:

 f (x) = g (x),
f (x) = g (x),
x  ,
,
 1. f
1. f  f (-x) = g (x),
f (-x) = g (x),
x < 0;
 |

 f (x) = g (x),
f (x) = g (x),
 f (x)
f (x) 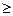 0 g (x)
0 g (x) 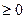 ,
,
 2.
2. 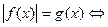
 f (x)= g (x),
f (x)= g (x),
-f (x) = g (x), f (x) = -g (x);
f (x) < 0
 |
f (x) = g (x),
3. 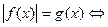
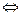 f
f  (x) = g
(x) = g  (x)
(x)
f (x) = -g(x)
4. 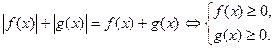
5. 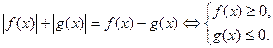
6. 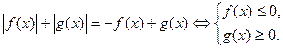
7. 
8. 
9. 
10.  ,
,
де  f
f 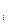 (x), i =
(x), i = 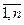 , g(x) – деякі функції.
, g(x) – деякі функції.
Часто розв’язування таких рівнянь послідовним розкриттям знаків модуля дуже громіздке. Такі рівняння найпростіше розв’язувати методом інтервалів. Для цього знаходять всі точки, в яких хоча б одна із функцій f 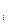 (x), i=
(x), i= 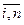 змінює знак. Ці точки ділять область допустимих значень рівняння на проміжки, на кожному з яких всі функції f
змінює знак. Ці точки ділять область допустимих значень рівняння на проміжки, на кожному з яких всі функції f 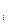 (x), і =
(x), і = 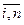 зберігають знак. Використовуючи означення модуля, переходять від рівняння до сукупності систем, які не містять знаків модулів.
зберігають знак. Використовуючи означення модуля, переходять від рівняння до сукупності систем, які не містять знаків модулів.
Аналогічно можна розв’язувати і відповідні нерівності:
 .
.