Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язання. Нерівності з великою кількістю лінійних виразів під знаками модулів зручно розв’язувати графічно, оскільки у цьому разі розкриття модулів за означенням
|
|
Нерівності з великою кількістю лінійних виразів під знаками модулів зручно розв’язувати графічно, оскільки у цьому разі розкриття модулів за означенням технічно ускладнює розв’язання задачі.
Обчислимо значення лівої частини нерівності в тих точках, де вирази під знаками модулів дорівнюють нулю.
| x |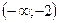 
| -2 | -1 |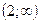 
| |||
| y | Y=-x | Y=x |
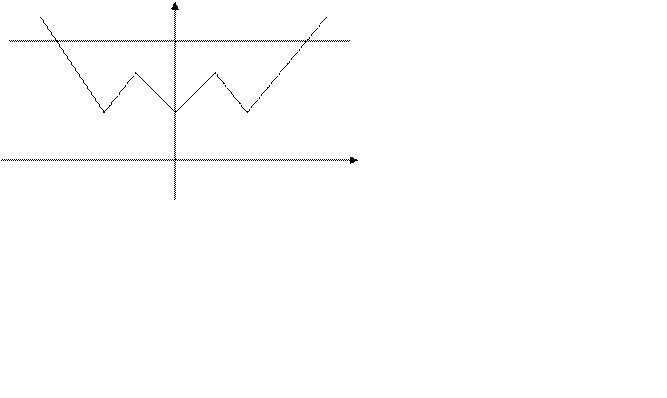
Графіком лівої частини буде неперервна ламана лінія, яку легко побудувати за виразами тільки на двох проміжках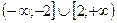 
і за значеннями 
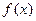в точках х=-2, -1, 0, 1, 2.
Відповідь: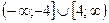 
ІІ. Нерівності виду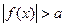 
або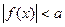 
.
При розв’язуванні таких нерівностей із знаком модуля можна користуватися наступними властивостями абсолютної величини:
1. Нерівність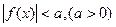 
рівносильна подвійній нерівності 
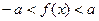, або, що те ж саме, системі нерівностей: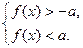 
2. Нерівність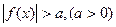 
рівносильна сукупності двох нерівностей: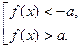 
У разі нестрогої нерівності усі знаки нерівностей доповнюються знаком рівності.