
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язання. Розглянемо два випадки.
|
|
Розглянемо два випадки.
Якщо 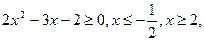 то отримаємо рівняння:
то отримаємо рівняння:
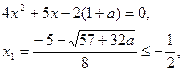
Виконується при  Більше двох цей корінь бути не може.
Більше двох цей корінь бути не може.
Для 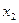 потрібно розв’язати дві нерівності:
потрібно розв’язати дві нерівності:

Перша нерівність виконується при 
а друга при 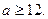
Розглянемо другий випадок, нехай:

Дане рівняння стає лінійним і ми знайдемо 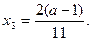
Розв’яжемо нерівність:

Отже при 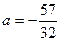 корені
корені  співпадають, а корінь
співпадають, а корінь  не існує, тобто рівняння має єдиний розв’язок
не існує, тобто рівняння має єдиний розв’язок 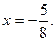
Якщо 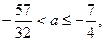 то рівняння має два різні розв’язки
то рівняння має два різні розв’язки  якщо
якщо  то
то 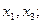 якщо ж
якщо ж 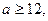 то два розв’язки
то два розв’язки 
Корені 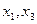 різні, так як
різні, так як 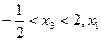 лежить поза цим інтервалом.
лежить поза цим інтервалом.
Відповідь: 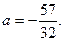
Системи рівнянь що містять абсолютну
Величину і параметри.
Приклад 1.
Розв’язати систему рівнянь:

Розв’язання
Якщо 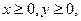 то отримаємо систему:
то отримаємо систему:

Якщо 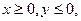 то
то 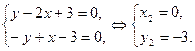
Якщо  то
то 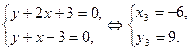
Якщо 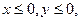 то
то 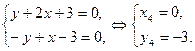
Кожні із чотирьох розв’язків задовольняють записані умови.
Відповідь: (2; 1); (0; -3); (-6; 9); (0; -3).