Розв’язування нестандартних завдань.

Приклад 1.

Розв’язати систему рівнянь:

Розв’язання

Враховуючи, що 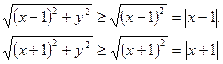та використовуючи геометричний зміст модуля, випливає, що 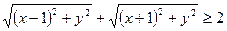для всіх х та у. Отже, рівність виконується при Тоді з другого рівняння системи отримуємо х=0.

Відповідь: (0; 0).

Приклад 2.

Розв’язати рівняння:

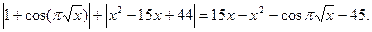
Розв’язання

Використовуємо властивість: якщо Тоді рівняння рівносильне системі:

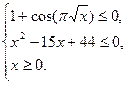
Оскільки для всіх х, то

при оскільки n – ціле, то n=0, 1, 2, 3, … Звідки

Отже, система набуває вигляду:

Відповідь: 9.

Приклад 3.

Розв’язати рівняння:

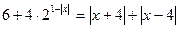
Розв’язання

Використовуючи геометричний зміст модуля, маємо:

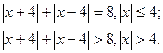
Отже, якщо 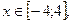то рівняння набуває вигляду:

Якщо 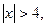то маємо: тобто що не задовольняє умову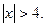

Відповідь: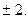

Приклад 4.

Розв’язати систему рівнянь: