Приклад 7.

Розв’язати нерівність:

Розв’язання

Отримаємо рівносильну нерівність, якщо кожний множник замінимо за властивістю:

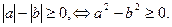
замінимо на

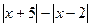замінимо на

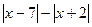замінимо на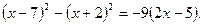

Тоді вихідна нерівність набуває вигляду:

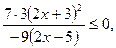розв’язками якої є: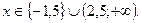

Відповідь:

Приклад 8.

Розв’язати нерівність:

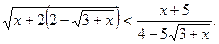
Розв’язання

Нехай 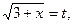тоді Отже нерівність набуває вигляду: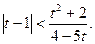

При маємо Розв’язки цієї нерівності з урахуванням умови звідки 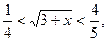тоді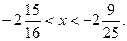

При маєм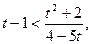о: тобто 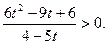Оскільки 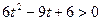для будь-яких t, то що не задовольняє умову

Відповідь:

Приклад 9.

Розв’язати рівняння:

Розв’язання

Областю визначення даного рівняння є: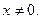

Використавши означення модуля, перетворимо дане рівняння у дві системи.

1)

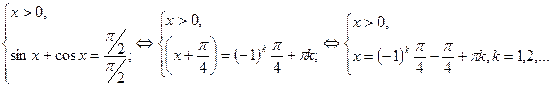
2)

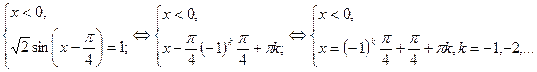
Відповідь:

Приклад 10.

Розв’язати рівняння: