Числовые характеристики функций многомерных случайных величин

Сформулированные в пункте 2.3.2 правила нахождения числовых характеристик функций одномерных случайных величин естественным образом обобщаются на случай функций от бó льшего числа переменных. В частности, если 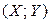– двумерный случайный вектор с известным законом распределения и 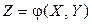, где 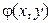– числовая функция скалярных аргументов x и y, то математическое ожидание и дисперсия случайной величины Z (если они существуют) могут быть найдены по следующим формулам:

,

если компоненты X и Y вектора 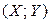являются СВДТ,

,

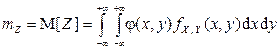если компоненты X и Y вектора 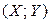являются СВНТ;

,

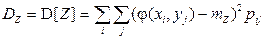если компоненты X и Y вектора 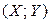являются СВДТ,

,

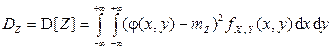если компоненты X и Y вектора 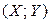являются СВНТ.

Аналогичные формулы имеют место и для всех прочих начальных и центральных моментов распределения случайной величины .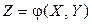

Замечание. Таким образом, для вычисления числовых характеристик функции многомерной случайной величины 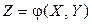необязательно знать закон распределения случайной величины Z, а достаточно знать закон распределения случайного вектора .

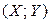Пример 2.3.18. Закон распределения случайного вектора 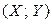задан таблицей:

Y X
–1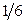

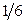
Не составляя закона распределения случайной величины , вычислить , .

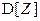Решение. Найдем вначале математическое ожидание:

.

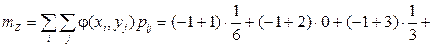
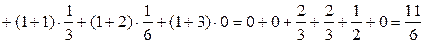Вычислим теперь дисперсию:

.

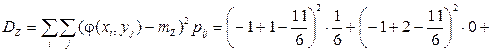
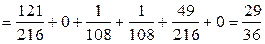Сравните найденные числовые характеристики случайной величины с аналогичными, полученными в примере 2.3.11.

Ответ: , .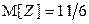

В пункте 2.2.7 рассматривались условные числовые характеристики случайных векторов. В частности, определялись условные математические ожидания двумерных случайных векторов 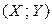. Напомним, что если случайные величины X и Y дискретны, то условные математические ожидания вычисляются по формулам:

, .

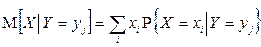Если случайные величины X и Y непрерывны, то условные математические ожидания вычисляются по формулам:

, .

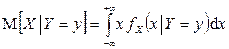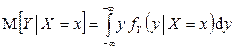Аналогично определяется условное математическое ожидание функции 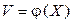при условии, что случайная величина Y приняла определенное значение (соответственно 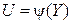при условии, что случайная величина X приняла определенное значение):

, ,

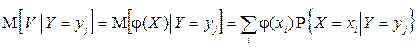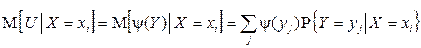если случайные величины X и Y дискретны;

, ,

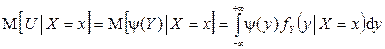если случайные величины X и Y непрерывны.

Также имеют место следующие формулы полного математического ожидания:

, ,

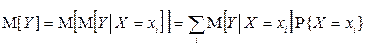если случайные величины X и Y дискретны;

, ,

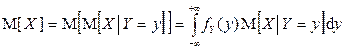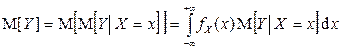если случайные величины X и Y непрерывны.

Пример 2.3.19. Число N радиотехнических приборов, сдаваемых покупателями в гарантийную мастерскую в течение дня, можно представить в виде случайной величины, хорошо описываемой распределением Пуассона 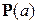, где a является средним числом приборов, сданных за день. Вероятность того, что сданный прибор потребует длительного ремонта, равна p. Найти среднее число приборов, требующих длительного ремонта.

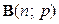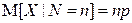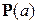Решение. При фиксированном числе n поступивших приборов количество приборов, требующих капитального ремонта, представляет собой случайную величину X с биномиальным распределением . Поэтому , . Поскольку случайная величина N имеет распределение Пуассона , то 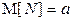. Тогда по формуле полного математического ожидания

.

Ответ: .