
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристическая функция
|
|
Если  – комплекснозначная случайная величина, где X и Y – действительные случайные величины, то
– комплекснозначная случайная величина, где X и Y – действительные случайные величины, то
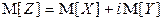 .
.
Определение. Характеристической функцией случайной величины X называется комплекснозначная функция
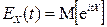 ,
,
где 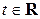 ,
, 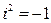 .
.
В частности,
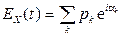 , если X – СВДТ;
, если X – СВДТ;
 , если X – СВНТ.
, если X – СВНТ.
Замечание 1. По характеристической функции 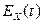 однозначно восстанавливается функция распределения
однозначно восстанавливается функция распределения 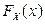 .
.
Замечание 2. Характеристическая функция представляет собой преобразование Фурье плотности вероятности 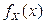 СВНТ X. Поэтому обратное преобразование Фурье приводит к соотношению
СВНТ X. Поэтому обратное преобразование Фурье приводит к соотношению
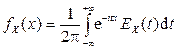 .
.
Таким образом, для СВНТ задание 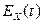 равносильно заданию
равносильно заданию 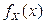 , и наоборот.
, и наоборот.
Характеристическая функция 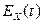 обладает следующими свойствами:
обладает следующими свойствами:
1. 
 .
.
2. 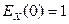 .
.
3. Если существует m -й абсолютный момент 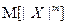 , то существуют производные характеристической функции
, то существуют производные характеристической функции 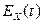 до m -го порядка включительно, причем
до m -го порядка включительно, причем 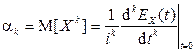 , где
, где 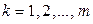 .
.
4. Если 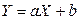 , то
, то 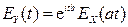 .
.
5. Если 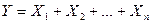 , причем
, причем 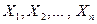 независимы в совокупности, то
независимы в совокупности, то  .
.
Замечание. Пользуясь этим свойством, можно решать задачу определения закона распределения суммы независимых случайных величин (задачи композиции). Действительно, если  , то
, то  . Найдя
. Найдя 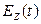 , можно по характеристической функции восстановить закон распределения случайной величины Z. Кроме того, по виду
, можно по характеристической функции восстановить закон распределения случайной величины Z. Кроме того, по виду 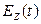 можно ответить на вопрос о композиционной устойчивости распределения.
можно ответить на вопрос о композиционной устойчивости распределения.
6.  , где черта означает операцию комплексного сопряжения. В частности, отсюда следует, что если
, где черта означает операцию комплексного сопряжения. В частности, отсюда следует, что если 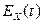 – действительная функция, то она обязательно четная.
– действительная функция, то она обязательно четная.
Определение. Характеристической функцией случайного вектора 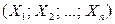 называется комплекснозначная функция n действительных переменных
называется комплекснозначная функция n действительных переменных 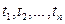 , определяемая равенством
, определяемая равенством
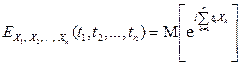 .
.
Пример 2.3.25. Найти характеристическую функцию случайной величины X, имеющей биномиальное распределение ( ), и с ее помощью вычислить
), и с ее помощью вычислить 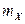 ,
, 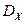 и
и  .
.
Решение. Согласно определению характеристической функции СВДТ X
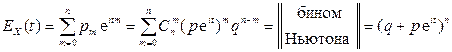 .
.
По свойству 3 для 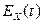 :
:

 ,
,

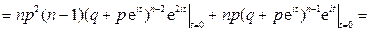
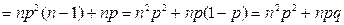 .
.
Отсюда
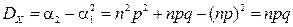 ,
, 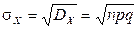 .
.
Пример 2.3.26. Найти характеристическую функцию случайной величины X, имеющей пуассоновское распределение (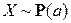 ), и с ее помощью вычислить
), и с ее помощью вычислить 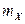 ,
, 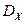 и
и  .
.
Решение. Согласно определению характеристической функции СВДТ X
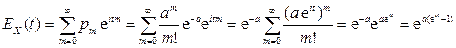 .
.
По свойству 3 для 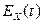 :
:
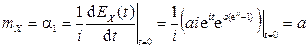 ,
,
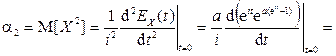
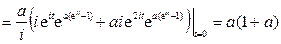 .
.
Отсюда
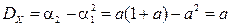 ,
, 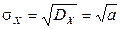 .
.
Пример 2.3.27. Найти характеристическую функцию случайной величины X, имеющей геометрическое распределение ( ), и с ее помощью вычислить
), и с ее помощью вычислить 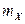 ,
, 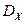 и
и  .
.
Решение. Согласно определению характеристической функции СВДТ X
 .
.
По свойству 3 для 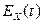 :
:
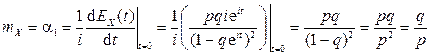 ,
,
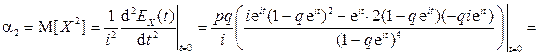
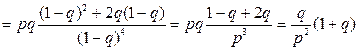 .
.
Отсюда
 ,
, 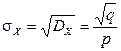 .
.
Пример 2.3.28. Найти характеристическую функцию случайной величины X, имеющей равномерное распределение (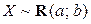 ).
).
Решение. Согласно определению характеристической функции СВНТ X
 .
.
Замечание. Для случайной величины 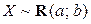 с помощью характеристической функции можно вычислить
с помощью характеристической функции можно вычислить 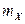 ,
, 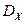 и
и  . Однако это не очень удобно, поэтому мы этого не делаем.
. Однако это не очень удобно, поэтому мы этого не делаем.
Пример 2.3.29. Найти характеристическую функцию случайной величины X, имеющей показательное распределение ( ), и с ее помощью вычислить
), и с ее помощью вычислить 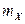 ,
, 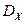 и
и  .
.
Решение. Согласно определению характеристической функции СВНТ X
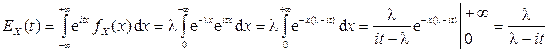 .
.
По свойству 3 для 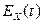 :
:
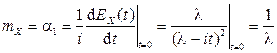 ,
,
 ,
,
Отсюда
 ,
, 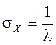 .
.
Пример 2.3.30. Найти характеристическую функцию случайной величины X, имеющей нормальное распределение ( ), и с ее помощью вычислить
), и с ее помощью вычислить 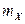 ,
, 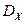 и
и  .
.
Решение. Найдем вначале характеристическую функцию случайной величины  . Согласно определению характеристической функции СВНТ X
. Согласно определению характеристической функции СВНТ X

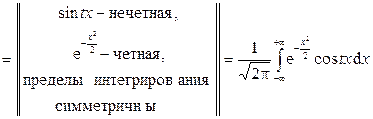
Дифференцируя 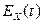 (по t) и применяя метод интегрирования по частям, получим:
(по t) и применяя метод интегрирования по частям, получим:
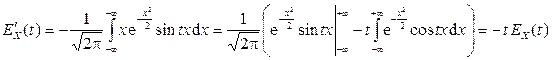 .
.
Решая это дифференциальное уравнение с разделяющимися переменными при начальном условии  (свойство 2 характеристической функции), находим
(свойство 2 характеристической функции), находим 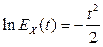 . Отсюда характеристическая функция случайной величины
. Отсюда характеристическая функция случайной величины  имеет вид
имеет вид
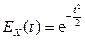 .
.
Рассмотрим теперь случайную величину  . Тогда нормированная случайная величина
. Тогда нормированная случайная величина  имеет нормальное распределение
имеет нормальное распределение  и, следовательно, характеристическую функцию
и, следовательно, характеристическую функцию 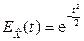 . Далее, по свойству 4 характеристической функции, для случайной величины
. Далее, по свойству 4 характеристической функции, для случайной величины 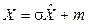 имеем
имеем
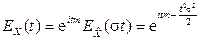 .
.
Найдем теперь математическое ожидание, дисперсию и среднее квадратическое отклонение  :
:
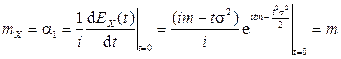 ,
,
 ,
,
Отсюда
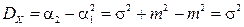 ,
,  .
.
Пример 2.3.31. Проверить композиционную устойчивость нормального закона.
Решение. Пусть независимые случайные величины X и Y имеют нормальное распределение: 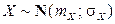 ,
, 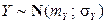 . Найдем
. Найдем 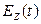 случайной величины
случайной величины  , учитывая свойство 5 характеристической функции и опираясь на результаты примера 2.3.30:
, учитывая свойство 5 характеристической функции и опираясь на результаты примера 2.3.30:
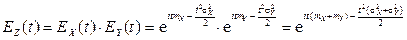 .
.
Откуда видно, что характеристическая функция 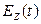 соответствует нормальному распределению, причем
соответствует нормальному распределению, причем  . Значит, нормальный закон является композиционно устойчивым.
. Значит, нормальный закон является композиционно устойчивым.