
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 2.3.13. СВНТ X имеет плотность вероятности
|
|
2.3.13. СВНТ X имеет плотность вероятности
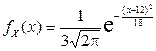 .
.
Найти  и
и  .
.
2.3.14. Плотность вероятности случайной величины X имеет следующий вид:
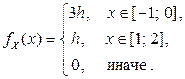
Найти 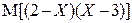 и
и 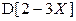 .
.
2.3.15. Пусть существуют дисперсии случайных величин X и Y такие, что  . Чему равна ковариация случайных величин
. Чему равна ковариация случайных величин 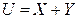 и
и 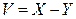 ?
?
2.3.16. Известно, что случайная величина 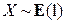 ,
, 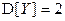 ,
, 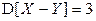 . Найти
. Найти 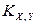 .
.
2.3.17. Известно, что случайная величина  . Пусть
. Пусть 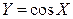 . Найти
. Найти 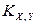 .
.
2.3.18. Известно, что случайные величины  ,
, 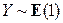 . Вычислить
. Вычислить 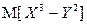 .
.
2.3.19. Подбрасывают три игральные кости. Рассматриваются случайные величины: X – количество костей, на которых выпало шесть очков, Y – количество костей, на которых выпало пять очков. Найти 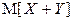 и закон распределения случайной величины
и закон распределения случайной величины  .
.
2.3.20. Предприятие имеет две поточные линии по сборке некоторой продукции. Технологические процессы на линиях связаны между собой. Рассматривая в качестве случайной величины X – количество единиц продукции, собранной за день на первой линии, а Y – на второй линии, совместное распределение этих величин можно задать с помощью таблицы:
| Y X | |||
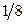
| 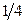
| 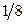
| |
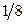
| 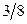
|
Составить закон распределения случайной величины  – суммарного количества единиц продукции, выпускаемой предприятием за день. Найти
– суммарного количества единиц продукции, выпускаемой предприятием за день. Найти  и
и 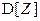 .
.
Ответы к упражнениям
2.3.13.  ,
,  .
.
2.3.14.  ,
, 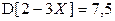 .
.
2.3.15. 0.
2.3.16. 0.
2.3.17. 0.
2.3.18.  .
.
2.3.19. 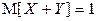 ,
, 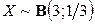 .
.
2.3.20.  ,
, 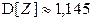 ; закон распределения Z:
; закон распределения Z:
| Z | ||||
| P | 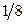
| 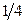
| 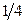
| 
|