
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Занятие 1-2. Линейные операции над векторами
|
|
Цель занятия: Усвоить понятия коллинеарные векторы, сумма и разность векторов, произведение вектора на число.
Задачи
1. Дан параллелепипед 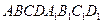 . Указать отрезки а) сонаправленные с отрезком
. Указать отрезки а) сонаправленные с отрезком  ; б) являющиеся представителем вектора
; б) являющиеся представителем вектора 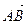 .
.
2. Точки  являются серединами сторон
являются серединами сторон 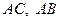 и
и 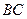 треугольника
треугольника 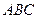 . Какие из пар векторов являются коллинеарными: а)
. Какие из пар векторов являются коллинеарными: а)  и
и 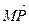 ; б)
; б) 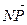 и
и 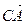 ; в)
; в) 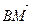 и
и 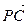 ; г)
; г) 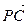 и
и 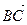 ; д)
; д) 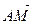 и
и 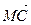 ; е)
; е) 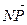 и
и  ; ж)
; ж) 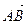 и
и 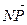 ?
?
3. В параллелепипеде 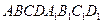 точки
точки 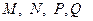 – середины ребер
– середины ребер  ,
, 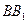 ,
,  и
и 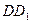 , а
, а 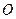 – точка пересечения диагоналей. Доказать, что а)
– точка пересечения диагоналей. Доказать, что а) 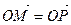 ; б)
; б) 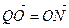 ; в)
; в) 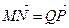 .
.
4. В параллелограмме 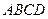 точка
точка 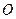 – точка пересечения диагоналей, а точки
– точка пересечения диагоналей, а точки  и
и  соответственно середины сторон
соответственно середины сторон 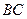 и
и 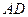 . Указать на чертеже представители следующих векторов: а)
. Указать на чертеже представители следующих векторов: а)  ;
;
б) 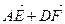 ; в)
; в) 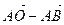 ; г)
; г) 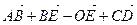 .
.
5. В параллелепипеде 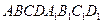 точки
точки  – середины ребер
– середины ребер 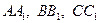 и
и 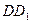 , точка
, точка 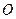 – точка пересечения его диагоналей. Указать на чертеже представители следующих векторов: а)
– точка пересечения его диагоналей. Указать на чертеже представители следующих векторов: а) 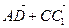 ;
;
б) 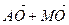 ; в)
; в) 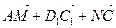 ; г)
; г) 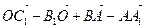 .
.
6. Пусть 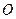 – центр правильного шестиугольника
– центр правильного шестиугольника 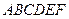 . Выразить векторы
. Выразить векторы 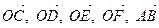 через векторы а)
через векторы а)  и
и  ; б)
; б) 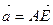 и
и 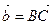 .
.
7. Даны векторы  и
и  . Построить векторы: а)
. Построить векторы: а) 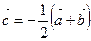 ; б)
; б) 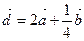 ; в)
; в) 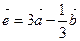 .
.
8. Доказать, что если 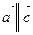 и
и 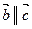 , и
, и 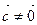 , то
, то 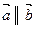 .
.
9. Доказать, что если 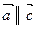 и
и 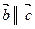 , то
, то 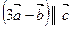 .
.
10. При каких условиях для ненулевых векторов  и
и  возможны следующие равенства: а)
возможны следующие равенства: а) 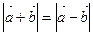 ;
;
б) 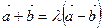 ; в)
; в) 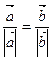 ?
?
11. Доказать, что для двух неколлинеарных векторов  и
и  вектор
вектор  делит пополам угол между векторами
делит пополам угол между векторами  и
и  .
.
12. В треугольнике 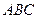
 – медианы. Выразить векторы
– медианы. Выразить векторы  через векторы
через векторы 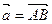 и
и 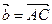 . Найти сумму векторов
. Найти сумму векторов  , дать геометрическую характеристику полученному результату. Доказать, что для любой точки
, дать геометрическую характеристику полученному результату. Доказать, что для любой точки 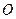 верно равенство
верно равенство 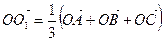 , где
, где 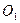 – центр тяжести треугольника.
– центр тяжести треугольника.
13. Какими должны быть векторы 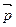 и
и 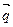 , чтобы векторы
, чтобы векторы 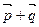 и
и 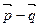 были а) ортогональны; б) равны по длине; в) коллинеарны; г) равны по длине и ортогональны?
были а) ортогональны; б) равны по длине; в) коллинеарны; г) равны по длине и ортогональны?
Домашнее задание
1. В параллелограмме 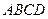
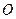 – точка пересечения диагоналей,
– точка пересечения диагоналей,  – середины сторон
– середины сторон  и
и 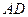 . Построить векторы: а)
. Построить векторы: а)  ; б)
; б) 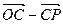 ; в)
; в)  ; г)
; г)  .
.
2. Точка 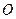 – центр правильного шестиугольника
– центр правильного шестиугольника 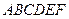 . Выразить векторы
. Выразить векторы 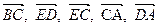 через векторы
через векторы  и
и 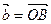 .
.
3. В треугольнике 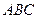
 и
и  – середины сторон
– середины сторон 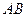 и
и 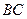 . Выразить векторы
. Выразить векторы  и
и  через векторы
через векторы 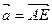 и
и 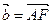 .
.