Занятие 17. Эллипс, гипербола, парабола

Цель занятия: Сформировать умения составлять канонические уравнения линий второго порядка.

Задачи

1. Найти уравнение окружности с центром 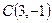, отсекающей на прямой 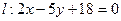хорду длины 6.

2. Найти уравнение окружности, касающейся прямых 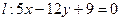и 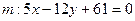, если 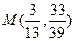– точка касания с прямой .

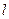3. Написать уравнение эллипса, если: а) его большая ось равна 10, а эксцентриситет равен 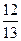; б) расстояние между директрисами равно 5, а расстояние между фокусами равно 4; в) расстояние между директрисами равно 32, а эксцентриситет равен .

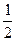4. Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.

5. Найти уравнение гиперболы, если: а) его асимптоты задаются уравнениями 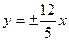, а расстояние между вершинами равно 48; б) расстояние между директрисами равно , а эксцентриситет равен ;
в) асимптоты задаются уравнениями 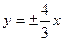, а расстояние между директрисами равно .

6. Вычислить площадь треугольника, образованного асимптотами гиперболы 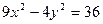и прямой .

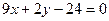7. Найти уравнение параболы, если: а) она расположена в полуплоскости, определяемой неравенством 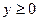, симметрична относительно оси 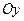и ее фокальный параметр равен 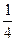; б) она расположена в полуплоскости, определяемой неравенством 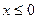, симметрична относительно оси 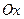и ее фокальный параметр равен .

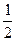8. Найти уравнение параболы с вершиной 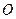, осью 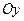и проходящей через точку .

9. Найти уравнение параболы с вершиной 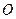, осью симметрии 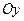и фокусом .

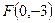10. Найти множество всех центров окружностей, проходящих через данную точку и касающихся данной прямой.

11. Найти множество всех точек плоскости, равноудаленных от данной точки и данной окружности.

Домашнее задание ИДЗ. Работа №4. Канонические уравнения конических сечений. [7]