Занятие 3-4. Линейная зависимость системы векторов. Базисы. Координаты вектора в данном базисе

Цель занятия: Усвоить понятия линейно зависимой и линейно независимой системы векторов, понятия базиса векторного пространства и координат вектора.

Задачи

1. Система векторов 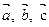является линейно независимой. Можно ли векторы , ,

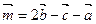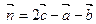принять в качестве базиса в пространстве?

2. Векторы 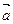и 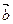неколлинеарны. Доказать, что система векторов 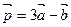, , 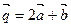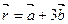является линейно зависимой. Найти координаты вектора 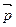в базисе .

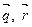3. Точка 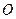– центр правильного шестиугольника 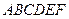. Найти координаты векторов в базисе .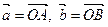

4. В параллелепипеде 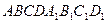точки 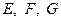– середины ребер 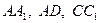. Найти координаты векторов 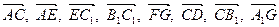в базисе , , .

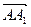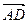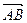5. Даны векторы 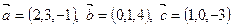. Определить координаты векторов:

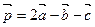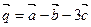а) ; б) ; в) .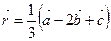

6. Можно ли выбрать в качестве базиса векторы:

а) ;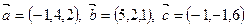

б) ?

Домашнее задание ИДЗ. Работа №1. Вектор и его координаты. [5].