
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Занятие 23-25. Решение задач элементарной геометрии координатным методом
|
|
Задачи
Продемонстрировать суть метода координат при решении задач
1. Доказать, что сумма квадратов расстояний от любой точки окружности до четырех вершин вписанного в нее квадрата равна учетверенной площади этого квадрата.
2. Доказать, что сумма квадратов расстояний от любой точки окружности до четырех вершин описанного около нее квадрата имеет одну и ту же величину.
3. Доказать, что сумма квадратов расстояний от любой точки окружности до трех вершин вписанного в нее равностороннего треугольника имеет одну и ту же величину.
4. Найти и построить геометрическое место точек, для которых сумма квадратов расстояний до двух вершин равностороннего треугольника равна квадрату расстояния до третьей вершины.
5. Найти и построить геометрическое место точек, для которых сумма квадратов расстояний до четырех вершин данного квадрата равна удвоенной площади этого квадрата.
6. Найти и построить геометрическое место центров окружностей, проходящих через данную точку и касающихся данной прямой.
7. Для трех данных точек 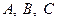 определить геометрическое место таких точек
определить геометрическое место таких точек 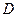 , что в четырехугольник
, что в четырехугольник 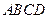 можно вписать окружность.
можно вписать окружность.
8. Найти множество всех точек плоскости, отношение расстояний от которых до двух заданных точек равно 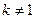 .
.
9. Найти множество всех точек плоскости, разность квадратов расстояний от которых до двух заданных точек равна 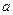 .
.
10. Определить множество середин всех отрезков, отсекаемых осями прямоугольной системы координат на прямых, проходящих через данную точку 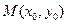 .
.
11. Доказать, что прямая, проходящая через точку пересечения боковых сторон трапеции и точку пересечения диагоналей трапеции, делит основания трапеции пополам.
12. Диагонали ромба равны 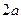 и
и 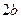 . Найти расстояние между противоположными сторонами ромба.
. Найти расстояние между противоположными сторонами ромба.
13. Доказать, что во всяком четырехугольнике точка пересечения прямых, соединяющих середины противоположных сторон, лежит на прямой, соединяющей середины диагоналей.
14. Доказать теорему Эйлера. Во всяком четырехугольнике сумма квадратов диагоналей равна сумме квадратов четырех его сторон без учетверенного квадрата расстояния между серединами диагоналей.
15. На прямой 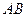 , проходящей через центр
, проходящей через центр 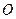 окружности радиуса
окружности радиуса 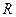 , отложены в обе стороны от центра отрезки
, отложены в обе стороны от центра отрезки 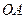 и
и 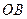 , равные диаметру. Доказать, что для любой точки
, равные диаметру. Доказать, что для любой точки 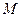 данной окружности сумма квадратов её расстояний до точек
данной окружности сумма квадратов её расстояний до точек 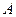 и
и 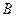 в 5 раз больше площади квадрата, вписанного в окружность.
в 5 раз больше площади квадрата, вписанного в окружность.
16. Доказать, что высоты треугольника пересекаются в одной точке.
Вариант контрольной работы по векторной алгебре
1. 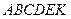 – правильный шестиугольник. Найти координаты векторов
– правильный шестиугольник. Найти координаты векторов 
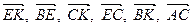 в базисе
в базисе 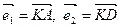 .
.
2. В треугольнике 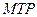 найти длину медианы
найти длину медианы  , если
, если 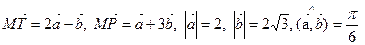 .
.
3. Найти высоту параллелепипеда 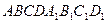 , если
, если 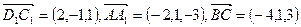 .
.
4. Какую часть объема призмы  составляет объем тетраэдра
составляет объем тетраэдра 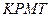 , если
, если 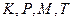 – середины ребер
– середины ребер 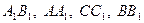 ?
?
Вариант тестового задания для контроля остаточных знаний
1. Дан правильный шестиугольник 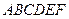 .
. 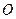 – точка пересечения его диагоналей. Сумма векторов
– точка пересечения его диагоналей. Сумма векторов 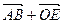 равна: а)
равна: а) 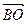 ; б)
; б)  ; в)
; в) 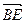 ; г)
; г) 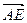 ; д)
; д) 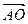 .
.
2. Найдите векторное произведение векторов 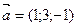 и
и 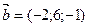 , если их координаты заданы относительно ортонормированного базиса.
, если их координаты заданы относительно ортонормированного базиса.
а) 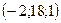 ; б)
; б) 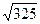 ; в)
; в) 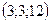 ; г)
; г) 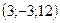 ; д)
; д) 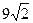 .
.
3. Заданы 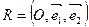 и точки
и точки 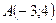 и
и 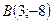 . Найдите координаты точки
. Найдите координаты точки  такой, что простое отношение точек
такой, что простое отношение точек 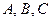 равно
равно 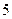 .
.
а) 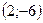 ; б)
; б) 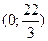 ; в)
; в) 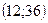 ; г)
; г) 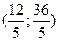 ; д)
; д) 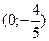 .
.
4. Общее уравнение прямой, проходящей через точку 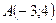 параллельно вектору
параллельно вектору 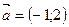 , имеет вид:
, имеет вид:
а) 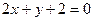 ; б)
; б) 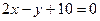 ; в)
; в) 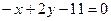 ;
;
г) 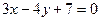 ; д)
; д) 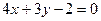 .
.
5. Относительно аффинной системы координат уравнение 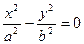 задает: а) эллипс; б) гиперболу; в) параболу; г) мнимый эллипс; д) пару пересекающихся прямых.
задает: а) эллипс; б) гиперболу; в) параболу; г) мнимый эллипс; д) пару пересекающихся прямых.
6. В треугольнике 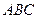
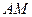 и
и 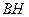 – медианы. Найдите координаты вектора
– медианы. Найдите координаты вектора 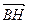 в базисе
в базисе 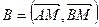 .
.
7. Составьте уравнения прямых, содержащих биссектрисы углов, образованных при пересечении прямых 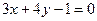 и
и 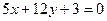 .
.
8. Составьте каноническое уравнение эллипса, если его малая ось равна 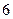 , а расстояние между фокусами равно
, а расстояние между фокусами равно 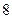 .
.
9. Вычислить координаты вершин ромба, если известны уравнения прямых, содержащих две его стороны: 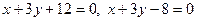 и уравнение прямой, содержащей его диагональ:
и уравнение прямой, содержащей его диагональ:  .
.
10. Составьте уравнение множества всех точек плоскости, расстояние от каждой из которых до точки 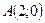 в два раза больше расстояния до прямой
в два раза больше расстояния до прямой  .
.
Литература
1. Атанасян, Л.С. Геометрия. Ч. 1: учеб. пособие / Л.С. Атанасян, В.Т. Базылев. – М.: Просвещение, 1986. – 336 с.
2. Атанасян, Л.С. Сборник задач по геометрии. Ч. 1 /Л.С. Атанасян, В.А. Атанасян. – М.: Просвещение, 1973. – 256 с.
3. Базылев, В.Т. Геометрия. Ч 1: учеб. пособие / В.Т. Базылев, К.И. Дуничев, В.П. Иваницкая. – Б.м.: Б.и., 2004. – 351 с.
4. Векторная алгебра и аналитическая геометрия в системе таблиц: сост. Т.А. Унегова. – Екатеринбург: УрГПУ, 1999. – 34 с.
5. Дидактические материалы по векторной алгебре: составители Г.А.Мазаева, Т.А.Унегова, Г.Ф. Шульгина. – Екатеринбург: УрГПУ, 1995. – 47 с.
6. Жафяров, А.Ж. Геометрия. Ч. 1: учеб. пособие / А.Ж. Жафяров. – Новосибирск: Сибирское университет. изд-во, 2002. – 271 с.
7. Индивидуальные задания по аналитической планиметрии: сост. Т.А. Унегова. – Екатеринбург: УрГПУ,. 1995. – 48 с.
Учебно-методическое издание
Геометрия. Материалы для практических занятий.
I курс, 1 семестр
Составители: