
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Абсолютная и относительная погрешности
|
|
Пусть А -точное значение некоторой величины, 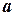 - известное приближение к нему, т.е. приближенное значение величины А. Обозначим
- известное приближение к нему, т.е. приближенное значение величины А. Обозначим 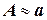 или
или 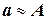 .
.
В зависимости от типа величины принято называть А точным числом, а его приближение 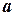 - приближенным числом. Например, в соотношениях
- приближенным числом. Например, в соотношениях
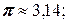
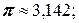
число  - является точным; числа 3, 14; 3, 142 – приближенные.
- является точным; числа 3, 14; 3, 142 – приближенные.
Разность 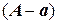 или (
или (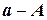 ) между точным и приближенным значениями величины называется погрешностью значения
) между точным и приближенным значениями величины называется погрешностью значения 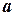 (но не А). Так как степень точности приближений удобно характеризовать с помощью неотрицательных чисел, вводится понятие абсолютной погрешности:
(но не А). Так как степень точности приближений удобно характеризовать с помощью неотрицательных чисел, вводится понятие абсолютной погрешности:
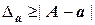 . (1)
. (1)
Знак (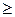 ) свидетельствует о том, что погрешность между А и
) свидетельствует о том, что погрешность между А и  не больше
не больше 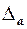 (но может быть и меньше). Действительно, совершенно неважно
(но может быть и меньше). Действительно, совершенно неважно  или
или 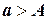 . Главное - насколько они отличаются.
. Главное - насколько они отличаются.
Абсолютная погрешность дает ценную информацию о неизвестном (часто) точном значении А: оно находится от известного приближения (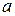 ) на расстоянии, не большем, чем
) на расстоянии, не большем, чем 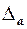 . Запись (1) можно представить иначе
. Запись (1) можно представить иначе
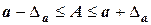 .
.
Следовательно, найдя приближенное значение 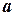 и его абсолютную погрешность
и его абсолютную погрешность 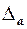 , узнаем, что точное значение А располагается на отрезке
, узнаем, что точное значение А располагается на отрезке 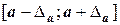 , но где точно - ответить на этот вопрос нельзя. Например, для измерения длины l болта использованы метровая линейка с делениями 0, 5 см и линейка с делениями 1 мм (0, 1 см). В обоих случаях получен результат
, но где точно - ответить на этот вопрос нельзя. Например, для измерения длины l болта использованы метровая линейка с делениями 0, 5 см и линейка с делениями 1 мм (0, 1 см). В обоих случаях получен результат 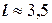 см. Ясно, что в первом случае отклонение найденной длины 3, 5 см от истинной не должно по модулю превышать 0, 5 см, во втором случае – 0, 1 см. Иначе, в первом случае
см. Ясно, что в первом случае отклонение найденной длины 3, 5 см от истинной не должно по модулю превышать 0, 5 см, во втором случае – 0, 1 см. Иначе, в первом случае 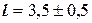 см, во втором случае
см, во втором случае 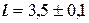 см. Очевидно, во втором случае измерение выполнено более точно. Отклонение
см. Очевидно, во втором случае измерение выполнено более точно. Отклонение
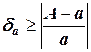 ;
; 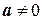
называется относительной погрешностью. Она позволяет оценить точность несопоставимых чисел. Часто используют соотношения:
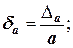
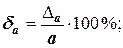
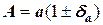 .
.
Если известна абсолютная погрешность 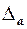 приближенного значения а, то а называется приближением к А с точностью до
приближенного значения а, то а называется приближением к А с точностью до 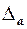 . Когда говорят, что надо получить результат с заданной точностью ε, это означает, что его абсолютная погрешность
. Когда говорят, что надо получить результат с заданной точностью ε, это означает, что его абсолютная погрешность 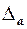 не должна быть больше ε.
не должна быть больше ε.