Метод касательных (метод Ньютона)

Рассматриваемый в данном разделе метод касательных и далее метод хорд относятся к методам последовательных приближений. Приближения к корню находят следующим образом: если известно предыдущее приближение 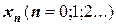, то последующее приближение 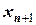вычисляют по формуле:

,

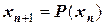где Р – некоторое выражение, устанавливающее связь между предыдущим и последующим приближениями. Формула вида 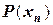называется рекуррентной формулой, а получаемую с ее помощью последовательность приближений называют итерационной последовательностью. Начинается процесс с какого-то числа 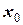(например, одна из границ отрезка существования корня) – начального приближения.

Рассмотрим более подробно первый метод – метод касательных. Предположим, непрерывная функция f(x) на отрезке (a; b) имеет один корень 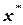(рисунок 9).

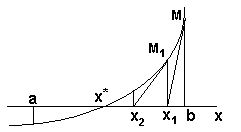
Рисунок 9 - К обоснованию алгоритма нахождения корня методом касательных

Это означает, что 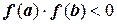. Проведем в точке М ( y=f(b )) касательную до пересечения с осью OX в точке 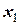.Очевидно, что

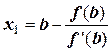, так как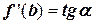

Видим, что точка x_1­ приблизилась к точке 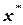от значения 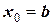на величину 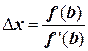. Если теперь поступить аналогично, получив на графике точку М₁ ( x₁ ), то очевидно, что можно получить следующее (более близкое к 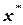) значение 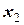, которое будет равно:

.

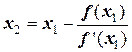Таким образом, в общем виде можем записать рекуррентную формулу:

.

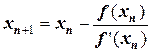Это базовая формула для получения ряда чисел x_i, которые будут приближаться к точному значению 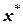. Величина 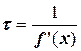называется релаксационным параметром. Он характеризует скорость сходимости. Чем он выше (чем более пологи линии касательных), тем быстрее скорость сходимости. Но в общем случае .

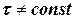Предположим, что в конечном итоге удается получить:

.

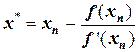Тогда в первом приближении 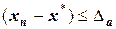- абсолютная ошибка приближения. Очевидно, что

.

Последовательность нахождения приближенного значения корня методом касательных следующая:

1) Продифференцировав искомую функцию, получают уравнение .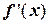

2) Составляют рекуррентную формулу.

3) Определяют интервал нахождения корня (a; b).

4) Одна из границ интервала принимается за начало итерационного процесса

(например, x₀=b).

5) Рассчитывают f(x₀) и f’(x₀).

6) По рекуррентной формуле получают очередное приближение корня:

.

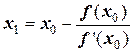7) Проверяют

.

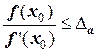При выполнении неравенства процесс вычислений прекращают.

8) В случае невыполнения неравенства расчеты по п.п. 4-7 повторяют.

В приложении Б представлена блок-схема алгоритма решения уравнения методом касательных (рисунок Б.2).

Задача 8. Найти приближенное значение корня с тремя верными цифрами для уравнения .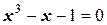

Решение. Как известно, корень этого уравнения находится на отрезке (1; 2), а требование получения трех верных цифр (с учетом данных, полученных в предыдущем примере) означает, что абсолютная ошибка должна быть не более 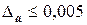. Составим расчетную таблицу, предварительно записав рекуррентную формулу в развернутом виде:

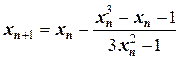или .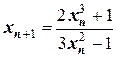

Таблица 5 - К вычислению корня уравнения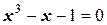

N n/n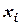
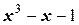
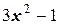
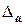
				0, 4545	1, 5454
	1, 5454	1, 14575	6, 1652	0, 1858	1, 3595
	1, 3595	0, 153448	4, 54519	0, 03376	1, 3257
	1, 3257	0, 004576	2, 977	0, 00153	1, 32417

Видим, что уже на третьем шаге итерации ошибка 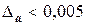, тогда значение корня будет 1, 324, где цифры 1, 3, 2 – верные, а цифра 4 – сомнительная.

Если сравнить два рассмотренных метода, то очевидно, что конечный результат достигается существенно быстрее и даже с более высокой точностью при применении метода касательных. Иногда он применяется в упрощенном варианте (так называемом модифицированном методе Ньютона), когда 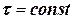. Это означает, что касательная, проведенная к граничной точке на кривой функции, в дальнейшем переносится параллельно самой себе и в отношении последующих точек на кривой.

Первоначально, для получения на нулевом шаге итерации, получают значение :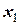

,

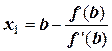но уже на втором и последующих шагах итерации угол наклона секущей (не касательной) остается постоянным и равным 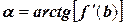, тогда рекуррентная формула примет вид:

,

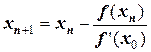где, например, .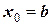

Такой упрощенный подход не требует вычисления значения производной 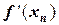на каждом шаге итерации, а позволяет использовать одно (первое) значение 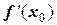. Это упрощает процедуру расчетов, но приводит к потере скорости сходимости и эффективность этого метода будет ниже, чем у классического метода Ньютона.