Оценка погрешностей приближения

Приближения 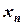, находимые методом хорд и касательных, стремятся к неизвестному корню 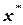с одной стороны. Поэтому так просто, как в методе деления пополам, проверить условие окончания итерационного процесса здесь не удастся. Необходимы специальные формулы оценки расстояния 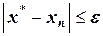, для вывода которых следует воспользоваться известной в математическом анализе теоремой Лагранжа.

Теорема Лагранжа. Если на отрезке ( x₀; x ) дана гладкая функция f(x), то между (x₀) и (x) всегда найдется хотя бы одна такая точка С (x₀< С< x), рисунок 12, что

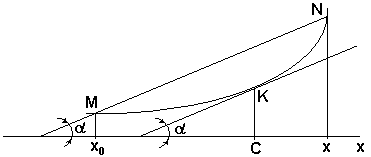
Рисунок 12 - К выводу формулы конечных приращений

будет верна формула:

.

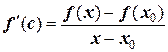Это формула конечных приращений Лагранжа. Геометрический смысл ее очевиден: если на графике функции f(x) через произвольно выбранные точки M( x₀; f(x₀) ) и N( x; f(x) ) провести хорду MN, то всегда можно найти на кривой функции точку K с абсциссой x=C, касательная к которой будет иметь тот же угол наклона 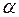, что и угол наклона хорды. Тогда, если при очередном шаге итерации получено приближенное значение корня х_п и соответственно известно значение f(x_n), то, соединив хордой точки ( x^*; 0 ), ( x_n; f(x_n) ), рисунок 13, можно воспользоваться формулой Лагранжа с учетом того, что ‌ ‌ (x_n – x^*)=∆ _a< ε.

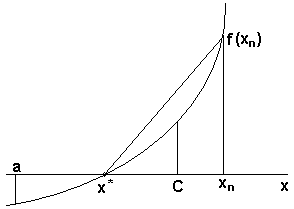
Рисунок 13 - К обоснованию вычисления погрешности

Если предположить, что для записи этой формулы положение точки С известно, формула Лагранжа примет вид:

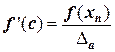или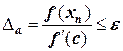

Остается проблема выбора точки С и соответственно значения f’(c). Очевидно, так как a< c< b, то возможно и неравенство f’(a)< f’(c)< f’(b). Введя величины f’(a)=m и f’(b)=M (принимается, что m< M), запишем .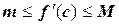

Применительно к методу хорд используются следующие формулы для расчета абсолютной погрешности

,

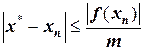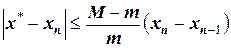
Наиболее часто пользуются первой формулой. Таким образом, если при нахождении приближенного значения корня методом хорд задана абсолютная погрешность 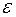, то итерационный процесс прекращают, когда достигается условие:

или .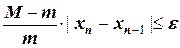

Замечание. Надо иметь в виду, что если отрезок (a; b) выбрать неудачно (например, слишком большим), дроб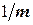и и 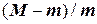могут оказаться настолько большими, что формулы (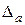) будут определять чрезмерно завышенные абсолютные погрешности приближений. Это также возможно, если т≈ 0 или М > > m. Применим метод хорд к решению ранее рассмотренной задачи.

Задача 9. Найти приближенное значение корня уравнения 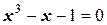не менее чем с тремя верными цифрами, воспользовавшись методом хорд.

Решение. Известно, что корень этого уравнения находится на отрезке (1; 2). Выполним предварительные вычисления.

1) При x=b вычислим значение функции:

.

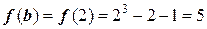2) Запишем рекуррентную формулу:

.

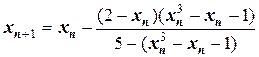3) Найдем уравнение производной:

.

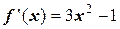Соответственно

; .

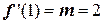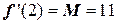4) Примем для расчета абсолютной погрешности .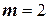

Тогда .

Соответственно .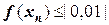

Составим расчетную таблицу и заполним ее.

Таблица 6 - Вычисление корня уравнения

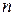
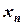
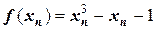
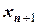
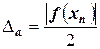
		-1	1, 1666	0, 5
	1, 16666	-0, 5787	1, 25311	0, 24
	1, 25311	-0, 28536	1, 2934	0, 14
	1, 2934	-0, 12954	1, 3111	0, 064
	1, 3111	-0, 05659	1, 31898	0, 028
	1, 31898	-0, 0243	1, 3222	0, 012
	1, 3222	-0, 01036	1, 3236	0, 0052
	1, 3236	-0, 00044	-	0, 0022

Видно, что три верные цифры 1, 3, 2 были получены в значении корня только на седьмом этапе итерации. Таким образом, значение корня равно .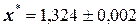

Примечание. Если принять для расчета погрешности вторую формулу, то, так как 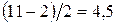, а 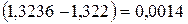, то абсолютная погрешность вычисления равна 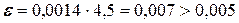. Следовательно, вторая формула дает более грубую ограничительную границу, что оправдывает сделанный выше выбор при оценке погрешности.

Под сходимостью понимается такая организация итерационного ряда x₀; x₁; x₂; …x_n, при которой его пределом будет точное значение корня 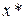. Говорят, что в таком случае «метод сходится». В противном случае метод расходится и получить нужное решение нельзя. Сходимость метода зависит прежде всего от трех факторов:

- основных признаков метода;

- величины интервала, на котором отделен корень;

- вида рекуррентной функции.

Сходимость определяется также скоростью, т.е. количеством итерационных шагов, необходимых для получения требуемого результата. Дадим характеристику каждого из рассмотренных выше методов

Метод половинного деления. Это наиболее устойчивый метод. Он всегда сходится, даже если на участке будет разрыв функции. К достоинствам метода следует также отнести и простоту расчета абсолютной погрешности. Метод имеет простой и легко реализуемый алгоритм. Имеет наименьшую скорость сходимости.

Метод Ньютона (метод касательных). Его применение требует от исполнителя более детального исследования функции в областях существования корня. Если касательная, проведенная в какой-либо точке, пересекает ось абсцисс вне интервала существования корня, то итерационный ряд расходится. Особенно часто это возможно, например, при анализе гармонической функции и при чрезмерно большом интервале. Однако из вышерассмотренных он имеет максимальную скорость сходимости.

Модифицированный метод Ньютона. Обладает всеми достоинствами и недостатками метода Ньютона, однако, так как 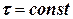, он имеет более низкую скорость сходимости по сравнению с методом касательных.

Метод хорд (секущих). Он всегда сходится, причем его скорость сходимости выше метода деления пополам, но ниже, чем у метода Ньютона.