Постановка задачи

Любая функция может быть представлена тремя способами:

- аналитически (с помощью математических символов)

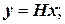
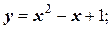
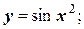
- в табличной форме:

- графически.

Решить уравнение – это найти значения аргумента х, при которых уравнение превращается в тождество 0=0.Графически это означает – найти значения х_i, в которых линия функции пересекает (или касается) ось абсцисс.

В курсах математики средней школы и математического анализа были рассмотрены принципы нахождения корней элементарных уравнений. Однако в практике, как правило, встречаются задачи, модели, решение которых в виде нахождения корней аналитическими методами невозможно.

Во-первых, уравнений, для которых существуют точные методы решения, сравнительно мало. Во-вторых, многие точные методы настолько трудоемки, что применять их нецелесообразно. В-третьих, очень часто точное решение уравнений и не является необходимым: проблема корня считается решенной, если найдено его приближение с заданной погрешностью.

Процесс приближенного решения уравнения распадается на два этапа: отделение корней и уточнение корней. Предположим, функция y=f(x) имеет два корня 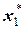и 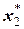. Отделить корни – это значит найти отрезок (или отрезки) а и b, с и d и т д., которому эти корни принадлежат, рисунок 1.

Отделение корней – большая самостоятельная задача, тем не менее достаточно успешно она решается на базе уже известных в математическом анализе методов. Некоторые из специфических методов отделения мы рассмотрим ниже.

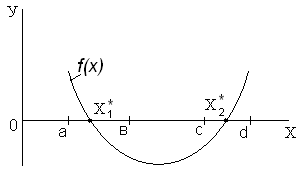
Рисунок 1 - К вопросу об отделении корня

После отделения корня его значение уточняется, при этом возможны два принципиальных подхода.

Путем определенных алгоритмов отрезок отделения (a-b) уменьшают по величине до тех пор, пока не будет достигнуто соотношение ,

где 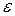- допустимая ошибка приближения корня 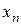(рисунок 2).

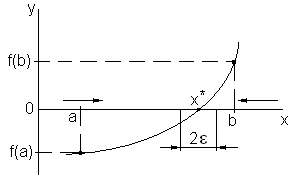
Рисунок 2 - Кинетика изменения интервала существования корня

Тогда можно утверждать, что истинное значение корня будет находиться в диапазоне

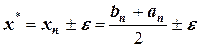
а величина 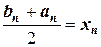- приближенное значение корня. Как будет показано ниже, условие 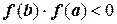является обязательным, гарантирующим соотношение 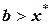, . Такой алгоритм можно классифицировать как двустороннее приближение.

Процесс уменьшения отрезка изоляции корня сопровождается появлением ряда чисел a₀; b₀; a₁; b₁; a­₂; b₂; …a_n, b_n, по которым будут рассчитаны значения

; ; …

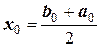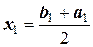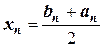
Этот ряд последовательно будет приближаться к истинному значению корня .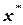

Другой алгоритм нахождения корня не предусматривает назначения интервала (а, b), в пределах которого ожидается нахождение корня, а на основании определенных соображений (в том числе и штатной процедуре отделения корня) назначается первоначальное отдаленное значение корня х_о, а затем, по результатам вычислений, выполняемых по определенному алгоритму, находят ряд чисел х₁, х₂, …, х_n-1, x_n, которые приближаются к истинному значению корня, т.е. f(x_i)→ 0, рисунок 3.

Рисунок 3 - Схема одностороннего приближения к корню

Приближение может быть как слева, так и справа, в зависимости от первоначального положения х_о относительно истинного значения х^* и продолжается до тех пор, пока не будет выполнено условие , но чаще условие окончания расчетного цикла имеет другой вид (см. ниже).