
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отделение корней
|
|
Отделение корней обычно производится графически и (или) аналитически. В общем случае процедура отделения корня уравнения 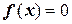 не может быть алгоритмизирована. Поэтому нередко отделение корней нелинейных уравнений выполняется «вручную» с использованием всей возможной информации о функции f(x). Иногда приближенное значение корня может быть определено из физических соображений, если нелинейное уравнение означает какую-либо конкретную прикладную задачу.
не может быть алгоритмизирована. Поэтому нередко отделение корней нелинейных уравнений выполняется «вручную» с использованием всей возможной информации о функции f(x). Иногда приближенное значение корня может быть определено из физических соображений, если нелинейное уравнение означает какую-либо конкретную прикладную задачу.
Графический метод отделения корней. Он обладает большой наглядностью и позволяет относительно просто устанавливать возможность существования кратных корней. Рассмотрим уравнение третьей степени:
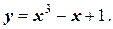
Если 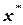 - корень уравнения, то очевидно, что y=0 при
- корень уравнения, то очевидно, что y=0 при  0=
0= 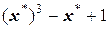 или
или
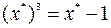 (2)
(2)
Обозначим
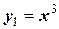 ;
;  .
.
Каждая из функций y1 и y2 достаточно проста, в том числе и в графической интерпретации. Изобразим 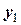 и
и  (см. рисунок 4).
(см. рисунок 4).
Корень уравнения (2) будет отвечать абсциссе точки М пересечения двух графиков 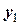 и
и  . В данном случае, очевидно, что уравнение
. В данном случае, очевидно, что уравнение 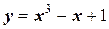 имеет только один корень и он находится на отрезке
имеет только один корень и он находится на отрезке 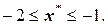
Табличный способ отделения корней. Рассмотрим еще один пример. Выполним процедуру отделения корня уравнения
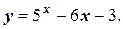 (3)
(3)
Представим эту функцию в виде двух функций:
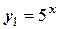 ;
; 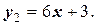
Очевидно, если 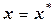 , то
, то 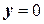 или
или  . Выделим ряд точек на числовой оси и вычислим значения функций
. Выделим ряд точек на числовой оси и вычислим значения функций 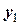 и
и  , а также их отношение. Результаты вычислений представим таблично (таблица 1).
, а также их отношение. Результаты вычислений представим таблично (таблица 1).
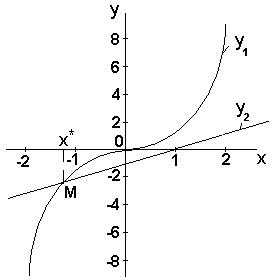
Рисунок 4 - Отделение корня нелинейного уравнения
Таблица 1 - К отделению корня уравнения 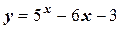
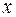
| 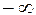
| -1 | 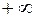
| |||
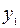
| 0, 2 | 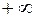
| ||||
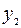
| 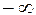
| -3 | 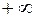
| |||
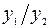
| 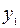 > > 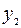
| 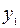 > > 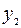
| 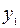 < < 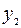
| 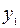 < < 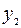
| 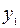 > > 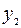
| 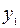 > > 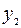
|
Можно построить графики функций 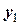 и
и  , но достаточно рассмотреть отношение
, но достаточно рассмотреть отношение 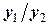 . Видим, что оно дважды изменяется по величине. Первый раз - на отрезке (-1; 0), второй раз - на отрезке (1; 2). Очевидно, что именно на этих отрезках должны находиться точки пересечения графиков двух функций. Поэтому можно утверждать, что уравнение (3) имеет два корня и они должны находиться на указанных выше отрезках (см. рисунок 5). Графический способ применяется наиболее часто. Обычно с него и начинают отделение корня, однако он не обладает большой точностью, и поэтому делать окончательно выводы на его основе не всегда удается.
. Видим, что оно дважды изменяется по величине. Первый раз - на отрезке (-1; 0), второй раз - на отрезке (1; 2). Очевидно, что именно на этих отрезках должны находиться точки пересечения графиков двух функций. Поэтому можно утверждать, что уравнение (3) имеет два корня и они должны находиться на указанных выше отрезках (см. рисунок 5). Графический способ применяется наиболее часто. Обычно с него и начинают отделение корня, однако он не обладает большой точностью, и поэтому делать окончательно выводы на его основе не всегда удается.
При отделении корня достаточно эффективно применение следующей теоремы:
Теорема 1. Если непрерывная функция f(x) определена на отрезке (a; b) и меняет знак, т.е. 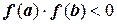 , то на этом отрезке содержится по крайней мере один
, то на этом отрезке содержится по крайней мере один






 Рисунок 5 - Отделение корня уравнения
Рисунок 5 - Отделение корня уравнения 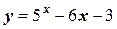
корень уравнения f(x)=0 или нечетное количество корней. Если же функция f(x) непрерывна и дифференцируема, и ее производная сохраняет знак внутри отрезка (a; b), то на этом отрезке находится только один корень уравнения f(x) =0. Действительно, как видно из рисунка 6а, при 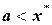
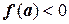 , при
, при 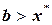
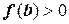 , следовательно,
, следовательно,
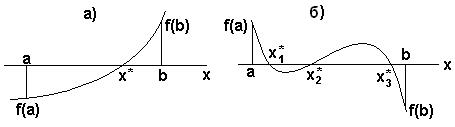
Рисунок 6 – Условия существования нечетного количества корней
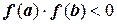 . На рисунке 6б при соблюдении условия
. На рисунке 6б при соблюдении условия 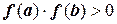 функция имеет три корня. Если же
функция имеет три корня. Если же 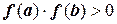 , то на этом отрезке либо корней нет, либо их четное количество (см. рисунок 7).
, то на этом отрезке либо корней нет, либо их четное количество (см. рисунок 7).
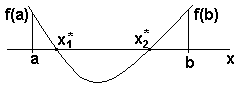
Рисунок 7 - Уравнение имеет два корня
Иногда для определения количества корней можно воспользоваться классическими методами исследования функции, рассматриваемыми в курсе математического анализа.
Задача 6. Отделить корни уравнения 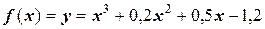 .
.
Решение. Продифференцируем это уравнение и получим другое (на порядок ниже):
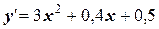 .
.
Видим, что второе уравнение имеет два корня, а соответственно первичная функция f(x) должна иметь два экстремума. При 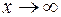 , очевидно, что
, очевидно, что 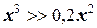 и тем более
и тем более 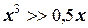 . Тогда можно утверждать, что при
. Тогда можно утверждать, что при 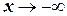
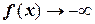 . При
. При 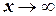 очевидно
очевидно 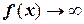 . Тогда становится ясно, что описываемая уравнением функция имеет седловидную форму, а искомое уравнение должна иметь по крайней мере один, а максимум три корня. Попробуем оценить значения функции в районе х=0 (табл.2).
. Тогда становится ясно, что описываемая уравнением функция имеет седловидную форму, а искомое уравнение должна иметь по крайней мере один, а максимум три корня. Попробуем оценить значения функции в районе х=0 (табл.2).
Таблица 2 - Значения функции 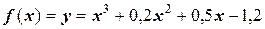
| x | 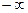
| -2 | -1 | 
| |||
| y | 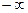
| -9, 4 | -2, 5 | -1, 2 | 0, 5 | 8, 6 | 
|
Очевидно, что корень уравнения должен уточняться на отрезке (a; b)=(0; 1), так как именно на этом отрезке происходит изменение знака функции.