
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Разрядность чисел, значащие и верные цифры
|
|
С помощью абсолютных погрешностей определяют так называемые верные и значащие цифры приближенных чисел.
Пусть приближенные число записано в виде десятичной дроби:
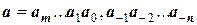 , т.е.
, т.е.
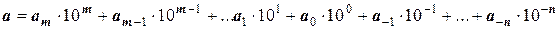 ;
;
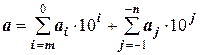 .
.
Степени (i j) называются «порядок числа», а число, равное 10i, называется разрядом числа. Очевидно, все целые числа от 0 до 9 – числа нулевого порядка (имеют разряд единиц, т.к. 100=1), от 10 до 99 – числа первого порядка (имеют разряд десятков, т.к. 101=10), от 100 до 999 – числа второго порядка (имеют разряд сотен, т.к. 102=100) и т.д. Если говорят, что данное число является (или должно быть) четвертого порядка, то это любое число от 10000 до 99999.
Все цифры дробной части (десятичной) записи числа, начиная с первой ненулевой цифры слева, называются значащими цифрами этого числа. Нули в конце числа всегда считаются значащими, в противном случае их не пишут. Например, числа 0, 5020 и 0, 05020 имеют одинаковые значащие цифры: 5; 0; 2; 0. Абсолютную погрешность не следует записывать с большим количеством значащих цифр. Основной информацией, содержащейся в ней, является значение первой ненулевой цифры и десятичный разряд, в котором эта цифра расположена (например, ± 0, 004, ±0, 0001).
Все значащие цифры подразделяются на верные и сомнительные. Их идентификация базируется на величине заданной погрешности числа.
Правило 1. Значащая цифра приближенного числа а называется верной, если она находится в разряде, половина которого больше абсолютной погрешности 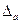 . Остальные цифры, для которых это правило не выполняется, считаются сомнительными.
. Остальные цифры, для которых это правило не выполняется, считаются сомнительными.
Задача 1. Для приближенного числа x=72, 356 известна абсолютная погрешность 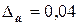 . Требуется определить его верные значащие цифры.
. Требуется определить его верные значащие цифры.
Решение. Выполним проверку на «верность» для каждой цифры числа.
1) Проверим цифру 7. Половина единицы ее разряда 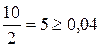 . Значит, она
. Значит, она
верная.
2) Проверим – цифру 2. Половина единицы ее разряда 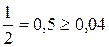 . Она тоже верная.
. Она тоже верная.
3) Цифра 3. Половина ее разряда 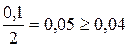 . Значит и она верная.
. Значит и она верная.
4) Цифра 5. Половина ее разряда 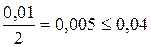 . Значит цифра 5 сомнительная, а соответственно сомнительна и цифра 6.
. Значит цифра 5 сомнительная, а соответственно сомнительна и цифра 6.
Итак, верными являются цифры 7; 2; 3. Остальные цифры – сомнительные.
Задача 2. Даны числа а, в, с и их абсолютные погрешности. Определить верные цифры.
а=2, 645 в=0, 81726 с=3968
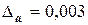
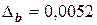
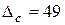 .
.
Решение.
В числе а верными будут числа 2, 6, 4, сомнительная одна цифра 5.
В числе в верной будет цифра 8, остальные сомнительные.
В числе с верными будут только цифры 3, 9, остальные сомнительные.
Таким образом, верные цифры в равноправной степени
- могут состоять только из нулей (например, если число 78, 00 имеет все верные цифры, значит оно записано с точностью до 0, 005) и тогда нули пишут обязательно;
- могут содержать и значащие цифры (например, число 78, 0051 с точностью до 0, 0005 имеет верные цифры после запятой 0; 0; 5, а число 1 сомнительное).
Нередко бывает так, что исходные числовые данные приводятся без оценки их погрешностей, но с известными верными цифрами. Возникает обратная задача: найти абсолютные погрешности этих чисел, необходимые для последующего учета погрешностей. Решение следует из определения верной цифры. Если дробная часть числа а=4, 06 содержит только верные цифры, то это означает, что 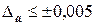 .
.
Правило 2: за абсолютную погрешность (если она не задана отдельно) приближенного числа с известными верными цифрами принимается половина единицы того разряда, где находится последняя верная цифра.
Обратим внимание на информационную значимость нулей, записанных в конце числа. Так, если известно, что все цифры чисел 3, 2 и 3, 20 верные, то эти записи неравноценны. За абсолютную погрешность первого числа можно взять 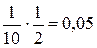 . Для второго
. Для второго 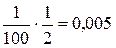 .
.
Правило 3: когда в конце числа получаются верные нули округления, их следует сохранять.
Пусть число а= -17, 298 с абсолютной погрешностью 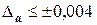 требуется округлить до верных цифр. Очевидно, что последней верной цифрой должна быть вторая после запятой, т.е. а= -17, 30, но не а= - 17, 3 (заметим, что в числе а=17, 30 нет сомнительных цифр). Но если для того же числа
требуется округлить до верных цифр. Очевидно, что последней верной цифрой должна быть вторая после запятой, т.е. а= -17, 30, но не а= - 17, 3 (заметим, что в числе а=17, 30 нет сомнительных цифр). Но если для того же числа 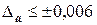 , округленное число будет а=17, 3.
, округленное число будет а=17, 3.
Очень часто, для облегчения понимания требований, предъявляемых к приближенному числу, применяют термин «точность». В числе, определяемом как точность, последняя правая цифра указывает на разряд последней верной цифры, например, в дробной части приближенного числа. Если приближенное число должно быть вычислено с точностью, например, до 0, 001, это означает, что в результате третья после запятой цифра должна быть верной, если точность оценивается числом 0, 01, то в дробной части вторая цифра после запятой должна быть верной. Заметим, что для выполнения первого требования число должно иметь абсолютную погрешность не более ±0, 0005, во втором случае – не более ±0, 005