
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление погрешностей при арифметических действиях
|
|
В практике вычислений, производимых с приближенными числами, неизбежно возникает вопрос о влиянии погрешностей исходных чисел на погрешность конечного результата. Рассмотрим эту проблему подробнее.
Предположим, что вычисляется сумма С приближенных чисел Аi, т.е.
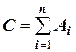 ,
,
где 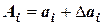 .
.
Искомую сумму можно записать так:
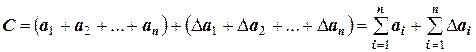 ,
,
или 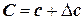 ,
,
где 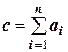 ,
, 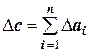 .
.
Правило 6: при сложении (вычитании) приближенных чисел результат является также приближенным числом, у которого абсолютная погрешность равна сумме абсолютных погрешностей всех слагаемых.
Относительная погрешность суммы рассчитывается следующим образом:
 .
.
Следует обратить внимание на то, что погрешность каждого слагаемого имеет знак (±), тем не менее при вычислении суммы (или разности приближенных чисел) погрешности слагаемых всегда записываются со знаком (+), но погрешность суммы ∆ с будет иметь знак (±).
Определим правило расчета погрешности произведения приближенных чисел. Для этого рассмотрим частную задачу – найдем произведение двух приближенных чисел
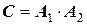 ,
,
где 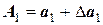 ,
, 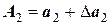 .
.
Запишем
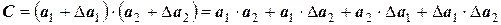 .
.
Так как из всех слагаемых последнее парное произведение является бесконечно малой величиной более высокого порядка, им можно пренебречь. Тогда, разделив вышеприведенное равенство на произведение 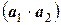 , получим
, получим
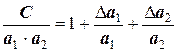 .
.
Заметив, что
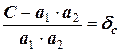 ,
, 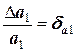 ,
, 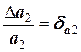 ,
,
получаем значение относительной погрешности произведения
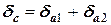 ,
,
значение абсолютной погрешности произведения
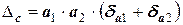 .
.
Эти выводы можно распространить на любое количество сомножителей. Действительно, если находится произведение приближенных чисел
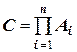 ,
,
где 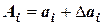 ,
, 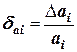 ,
, 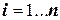 ,
,
то 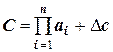 ,
,
где 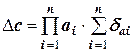 ,
, 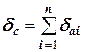 .
.
Правило 7. При умножении приближенных чисел результат будет иметь относительную погрешность, равную сумме относительных погрешностей сомножителей, а абсолютная погрешность произведения должна вычисляться через относительную по общему правилу.
Из последнего правила можно, как частный случай произведения, получить зависимости для расчета погрешности при возведении приближенного числа в степень (равно как и вычислении корня из приближенного числа). Действительно, если вычисляется
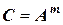 ,
,
где 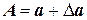 ,
, 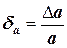 ,
,
тогда 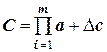 .
.
Учитывая, что 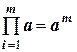 , а
, а 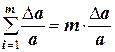 ,
,
запишем
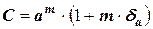 ,
,
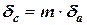 ,
,
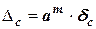 .
.
Задача 4. Определить, какое равенство записано точнее
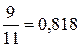 или
или 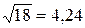 .
.
Решение. Находим значения равенств с большим числом десятичных знаков:
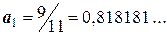 ,
, 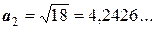 .
.
Затем вычисляем абсолютные погрешности:
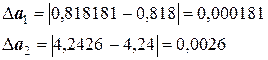
Если увеличивать количество десятичных знаков после запятой, вычисляя а1 и а2, соответственно также будут увеличиваться количество десятичных разрядов и у погрешности. Поэтому можно перейти к так называемым предельным абсолютным погрешностям:
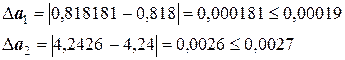 .
.
Абсолютные погрешности не позволяют провести сравнительный анализ двух вычислений на точность. С этой целью следует рассчитать относительные погрешности. Они будут равны:
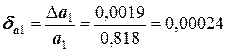 или
или 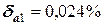 ,
,
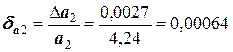 или
или 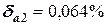 .
.
Очевидно, что первое вычисление выполнено с более высокой точностью, чем второе. Следовательно, только относительные погрешности позволяют сделать сравнительный анализ на достигнутую точность вычислений, причем на этот анализ не влияют ни абсолютные значения чисел, ни их размерность.
Задача 5. Вычислить и определить погрешности результата:
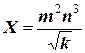
при следующих значениях величин:
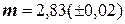 ,
, 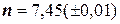 ,
, 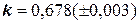 .
.
Решение. Находим результаты вычислений
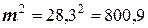 ,
, 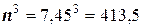 ,
, 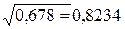 ,
,
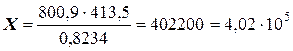 .
.
Рассчитываем относительные погрешности исходных чисел:
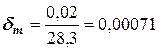 ,
, 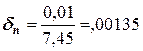 ,
, 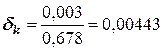 .
.
Рассчитаем погрешность результата:
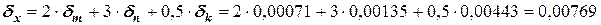 ,
,
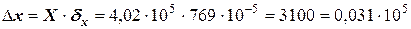 .
.
Ответ: 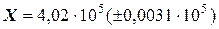 ;
; 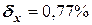 .
.