Итерации

Выше уже было показано, что для метода простой итерации важен способ записи уравнения 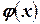в рекуррентной формуле. Кроме того, если у базового уравнения f(x)=0 корень не единственный, то для каждого из них, возможно, потребуется различная запись уравнения 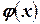. Необходимы навыки его получения с такими значениями | 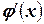| в окрестности корня, чтобы выполнялось услови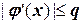е , где 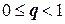. Если самая простая форма 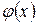дает процедуру расхождения, надо рассмотреть другой вид функции 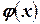. Наиболее часто используется следующий способ.

Пусть дано уравнение f(x) с единственным корнем на отрезке [ a; b ]. Предположим, что на этом отрезке функция f(x) непрерывна, не равна константе и первая производная принимает значение одного и того же знака. Будем, для простоты, считать, что f’(x)> 0, иначе можно рассматривать равносильное уравнение - f(x)=0.

Обозначим предельные значения производной 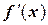на расчетном отрезке

; ,

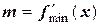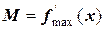а также введем коэффициенты 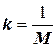и .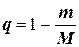

Ясно, что 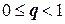, так как (М-т)< М.

Будем искать уравнение в виде

.

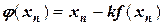Для этого уравнения всегда выполняется условие 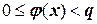при любых x в интервале (a; b). Тогда рекуррентная формула 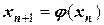примет вид:

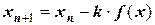. (6)

Если в этом выражении проанализировать смысловое содержание коэффициента k (как величины, обратной производной от искомой функции на расчетном интервале), то становится очевидной связь двух методов – модифицированного метода Ньютона и метода простой итерации. В последнем случае секущая будет иметь усредненное значение угла наклона. Следует также иметь в виду, что значение коэффициента k всегда подставляется в уравнение y(x) со своим знаком.

В отдельных случаях коэффициент k выбирают в пределах 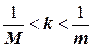, но достаточно часто принимают 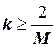. Также надо помнить, что успех сходимости итерационного процесса в существенной степени зависит от величины отрезка (a; b). Чем он меньше, тем надежнее процесс сходимости.

Задача 12. Найти корень уравнения 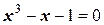методом простой итерации с точностью до 0, 001.

Решение. Ранее было показано, что корень этого уравнения находится на отрезке (1; 2). На основе функции 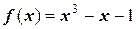можно построить очевидную итерационную формулу 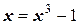. Если принять 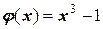, то 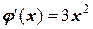и тогда 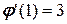; 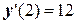. Это означает, что 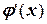на участке нахождения корня значительно больше единицы и, следовательно, процесс итерации будет расходиться.

Для успешного решения найдем другой вид итерационной формулы. Применим описанный ранее способ. Прежде всего найдем значения производных от первичной функции f(x) на концах расчетного отрезка:

,

, .

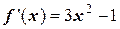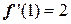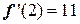Следовательно, m=2; M=11.

Применим следующую рекуррентную формулу (6),

где .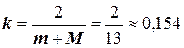

Тогда

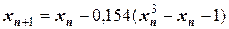
или .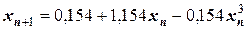

Решение дает следующие результаты:

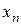
		1, 23	1, 28684	1, 31084	1, 31984	1, 32303
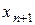
	1, 23	1, 2868	1, 31084	1, 31984	1, 32303	1, 32413

Видим, что на шестом шаге итерации получили значение корня 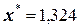, что совпадает с ранее выполненными расчетами.

Для метода простой итерации принимается следующая формула для расчета погрешностей вычисления. Если задана точность приближенного корня 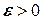, то итерационный процесс необходимо закончить при выполнении условия:

,

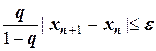где ,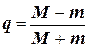

а значение корня принимается равным 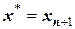.