Метод итерации для систем линейных уравнений

Итерационные методы позволяют получить решение с наперед заданной точностью, если доказана сходимость метода. Строго точного решения итерационные методы не дают, поскольку оно достигается как предел последовательности векторов промежуточных решений. Прямой метод, вообще говоря, дает точное решение, но из-за ошибок округления, имеющих место на любых компьютерах, оно не может быть достигнуто, и заранее его даже трудно оценить, насколько это решение отличается от точного. Поэтому итерационные методы иногда позволяют получить решение с большей точностью, чем прямые, и менее трудоемким способом.

Пусть дана система (7) из п уравнений с п неизвестными. Чтобы построить итерационный процесс приближения к точному решению, ее предварительно приводят к эквивалентной системе:

.

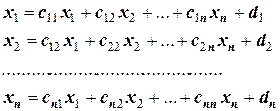Назовем эту систему приведенной. Обозначив

, , ,

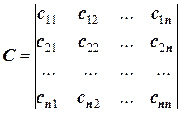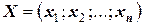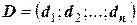ее можно записать в матричной форме:

.

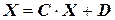Покажем два способа преобразования первичной системы к приведенной.

Пусть дана система общего вида:

.

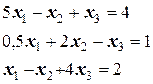Способ 1. Разделим каждое из приведенных уравнений на коэффициент при неизвестном 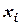, где =1, 2, 3 – номера переменной и уравнения. В результате получаем:

.

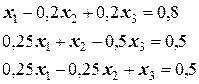Перепишем уравнения следующим образом:

,

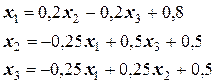Они образуют систему уравнений типа 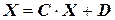, для которой матрица С имеет вид:

.

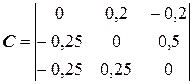Способ 2. Вычленим единицу из каждого диагонального коэффициента (например, 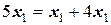) и выразим полученные таким образом 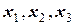из 1, 2 и 3-го уравнений соответственно:

.

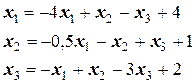В этой приведенной системе

.

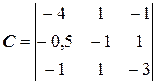Приведенные системы уравнений отвечают векторной форме 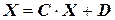и неизвестные вычисляются по реккурентной формуле:

.

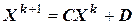Так, взяв какой-либо вектор 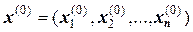и подставив его координаты в правую часть системы, получим новый вектор 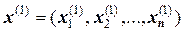. Действуя далее по аналогичной схеме, получаем итерационную последовательность для системы уравнений. Процесс остановливают по достижении требуемой погрешности.

Важнейшей проблемой решения системы линейных уравнений итерационным методом является сходимость процесса. Уже рассмотренные выше два способа преобразования базовой системы уравнений дали две сильно отличающиеся приведенные системы. Вряд ли следует ожидать их “равноправность” с точки зрения достижения результативности процесса итерации. Не останавливаясь на теоретических основах проблемы сходимости, сошлемся на следующую теорему:

Теорема. Если матрица С коэффициентов при неизвестных в правой части преобразованной системы уравнений удовлетворяет условию

,

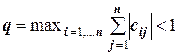то эта система имеет единственное решение Х^*, а построенная последовательность 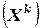сходится к Х^* при любом начальном приближении Х.

Иначе, теорема гласит, что наибольшая из сумм модулей коэффициентов при неизвестных в правой части преобразованной системы, вычисленных по каждой строке, дожна быть меньше единицы. Очевидно, это возможно лишь тогда, когда все элементы матрицы С достаточно малы по модулю. Например, в рассмотренном выше примере удовлетворяет этому условию только система, полученная по первому способу, так как для нее

.

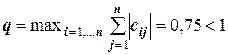Для второго способа преобразования это условие будет иметь вид:

.

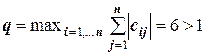Следовательно, преобразованная по первому способу система линейных уравнений будет сходиться, по второму способу – нет.

Существуют различные приемы преобразования исходной системы уравнений к виду, удобному для осуществления итерационного процесса. Выше приведены только наиболее простые и очевидные. Для применения первого способа необходимо, чтобы диагональные коэффициенты исходной системы не равнялись нулю и были намного больше по модулю остальных коэффициентов соответствующих уравнений. Такая ситуация имеет место в рассмотренном выше примере.

Когда диагональные коэффициенты близки к единице, а остальные коэффициенты малы по модулю, подойдут оба способа. Но второй способ предпочтительнее, так как он не связан с делением. Эти способы можно применять как в целом к системе, так и к отдельным уравнениям, переставляя (при необходимости) уравнения.

Важной характеристикой итерационного процесса является скорость сходимости вычислений, что и определяет его экономичность. Применительно к системе уравнений разработаны различные методы их решения. Если отталкиваться от очевидного (прямого) метода итерации, когда параметры вектора Х^(j) подставляются в приведенную систему уравнений, можно рассмотреть и другой метод, называемый методом итераций Зейделя. Сущность его заключается в том, что в первое уравнение приведенной системы вводятся исходные параметры вектора Х^(j), а в последующие уравнения постепенно вводятся параметры переменных, вновь вычисленные в предварительно решенных уравнениях. Не вдаваясь в подробности, отметим, что метод Зейделя часто действительно приводит к более быстрой сходимости, чем метод простой итерации. Однако возможны случаи, когда метод Зейделя сходится медленнее, и даже случаи, когда метод простой итерации сходится, а Зейделя - расходится.

Задача 15. Найти решение системы линейных уравнений, приведенной выше, применив два метода итераций – простой и по Зейделю.

Решение. Пользуясь теоремой о сходимости процесса итераций для системы линейных уравнений, за основу возьмем преобразованную систему, полученную по первому способу преобразования. В качестве первичного вектора переменных примем 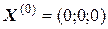. Тогда, по методу простой итерации получим первый вектор (он состоит из свободных членов уравнений): 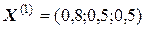. По методу Зейделя:

а) в первое уравнение введем значения вектора 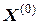и получим ;

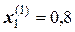б) во второе уравнение введем вновь полученное значение 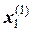, а :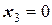

;

в) в третье уравнение введем вновь полученные значения 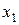и :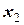

.

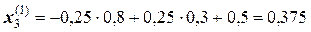Таким образом, имеем первый вектор .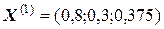

Полагая, что из сказанного выше алгоритмы расчетов понятны, приведем в табличной форме результаты расчетов переменных по шести итерационным шагам.

Таблица 15 - Результаты расчетов корней системы линейных уравнений в задаче 15

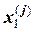
	0, 800	0, 8000	0, 8250	0, 8150	0, 8181	0, 8166
0, 88	0, 8250	0, 8150	0, 8180	0, 8171	0, 8169
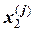
	0, 500	0, 5500	0, 5125	0, 5125	0, 5072	0, 5077
0, 550	0, 5125	0, 5150	0, 5080	0, 5069	0, 5070
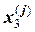
	0, 500	0, 4250	0, 4375	0, 4219	0, 4244	0, 4224
0, 425	0, 4375	0, 4250	0, 4225	0, 4224	0, 4225

Примечание: в верхней строке по каждому переменному приведены результаты расчетов по методу простой итерации, в нижней – итерации по методу Зейделя.

Точное решение исходной системы уравнений, полученное методом Гаусса, следующее: .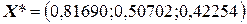

Представляет интерес сравнить два метода по величине погрешности и скорости процесса сходимости. В таблице 16 представлены проценты относительных погрешностей вычислений по каждому текущему результату. Из таблицы видно, что

Таблица 16 - Относительная погрешность вычислений корней системы в задаче 15

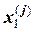
	-2, 07	-2, 070	+0, 980	-0, 230	+0, 150	-0, 041
-2, 07	+0, 980	-0, 230	+0, 130	-0, 012	0, 000
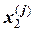
	-1, 384	+8, 470	+1, 010	+1, 010	+0, 030	+0, 125
+8, 470	+1, 010	+1, 570	+0, 200	-0, 023	-0, 012
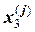
	+11, 830	+0, 585	+3, 540	-0, 155	+0, 437	-0, 035
+0, 585	+3, 540	+0, 585	-0, 010	-0, 037	-0, 003

в рассмотренном случае оба метода обеспечивают сходимость, причем метод Зейделя безусловно имел более высокую скорость.