
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полином Лагранжа
|
|
Если функция  задана в табличной форме (см. таблицу 17), то интерполяционный многочлен можно получить преобразованием полинома Лагранжа, имеющего следующий вид:
задана в табличной форме (см. таблицу 17), то интерполяционный многочлен можно получить преобразованием полинома Лагранжа, имеющего следующий вид:
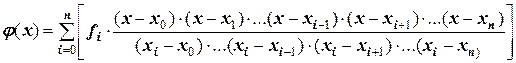 .
.
Полином Лагранжа – это сумма произведений i-го значения функции и дроби, числитель которой представляет собой произведение разностей между переменной (х) и всеми узлами, кроме i-го, а знаменатель – произведение разностей между i-ым узлом и всеми остальными.
Полином является универсальной конструкцией алгебры, на базе которого в дальнейшем были разработаны другие полиномы (см. ниже).
Задача 17. Произвести интерполяцию таблично заданной функции полиномом Лагранжа:
| х | 0, 5 | 1, 0 | 1, 5 | 2, 0 |
| f | 2, 75 | 4, 0 | 8, 75 |
Решение. Запишем полином Лагранжа для заданной функции. Он будет иметь вид:
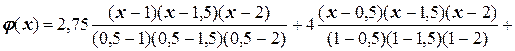
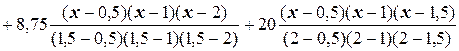 .
.
Если выполнить дальнейшие арифметические действия, то в результате получим:
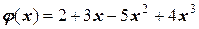 ,
,
т.е. тот же многочлен третьей степени, который был получен решением системы линейных уравнений.