Применение интерполяции к точечным расчетам значений функции

Рассмотрим следующую задачу. Пусть функция задана таблично в узловых точках 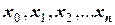. Надо найти значение функции 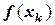при условии, что 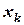не совпадает ни с одной узловой точкой. Эту задачу можно решить, пользуясь методом интерполяции функции. Однако в таком случае возникает естественный вопрос: для того, чтобы получить максимальную точность результата, как провести интерполяцию функции? Иначе, надо дать ответ на два вопроса:

а) сколько интервалов нужно выбрать для интерполяции (из имеющихся);

б) как расположить интересующую нас точку расчета относительно намеченных интервалов.

Заметим, что количество интервалов автоматически отвечает и на очевидный вопрос – какова должна быть степень интерполирующего многочлена.

Решение первичной задачи включает следующие этапы. Первый шаг заключается в расчете необходимого количества отрезков, на базе которых в дальнейшем должна проводиться интерполяция. При известном значении приближения 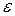по формуле ее расчета (см. предыдущий раздел) путем последовательной подстановки количества отрезков ( 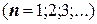получают приближение, не хуже заданного. Затем, пользуясь табличной записью функции, накладывают на нее расчетное количество отрезков, но так, чтобы значение 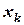располагалось примерно в центре этих отрезков. Таким образом минимизируется погрешность вычисления функции в заданной точке с помощью интерполяционной функции.