Задача приближенного вычисления определенных интегралов

В приложениях математики одной из наиболее часто встречающихся задач является вычисление определенного интеграла

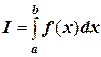
от некоторой интегрируемой на отрезке 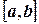функции f. Будем считать далее 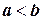, поскольку, если 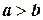, то можно перейти к интегралу с противоположным знаком. В курсе математического анализа доказывается, что, когда f непрерывна на отрезке 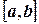, для нее существует первообразная F:

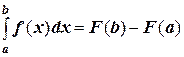, где .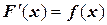

Это известная формула Ньютона-Лейбница, позволяющая произвести точное вычисление определенного интеграла. Однако в реальности использовать ее удается не всегда. Она неприменима для так называемых неберущихся интегралов, т.е. таких, у которых подынтегральные функции не имеют выражающихся через элементарные функции первообразных. Она малоэффективна, когда первообразная существует, но ее отыскание требует сложной процедуры. Кроме того, на практике часто приходится вычислять интегралы от табличных функций. Если при этом аналитическое выражение f неизвестно (например, функция задана таблично), формула Ньютона-Лейбница также бесполезна. В таких случаях применяются приближенные методы интегрирования, которые можно подразделить на аналитические и численные.

Аналитические методы. Их суть состоит в замене подынтегральной функции f на отрезке 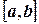некоторой аналитически заданной функцией 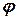, чью первообразную нетрудно найти. Тогда имеет место приближенное равенство:

.

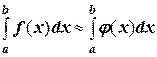Например, если разложить функцию f на отрезке 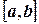в степенной или тригонометрический ряд, то в качестве можно взять частичную сумму этого ряда. Легко решается проблема, если функция f(x), представленная таблично, проинтерполирована на отрезке 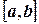, например, степенным многочленом (либо проведена кусочная интерполяция). В силу очевидной простоты получения интеграла в таких случаях в дальнейшем эти методы не рассматриваются.

Численные методы. Они позволяют обходиться без аналитических построений. Приближение к интегралу отыскивается по обобщенной расчетной формуле на основе числовых значений подынтегральной функции, вычисленных в конечном множестве точек на отрезке интегрирования. Такой способ вычислений часто называют механической квадратурой. Соответствующие приближенные формулы называют формулами численного интегрирования или квадратурными формулами, а используемые при этом аргументы функции – узлами квадратуры. Такая терминология отражает цель и основной принцип вычисления определенного интеграла. Определенный интеграл – это численное выражение площади, ограниченное осью абсцисс, графиком функции f(x) и вертикальными отрезками f(a), f(b). А, как известно, площадь фигуры с любой сложно заданной конфигурацией всегда можно вычислить приближенно с наперед заданной точностью, разбив ее на малые, но легко вычисляемые площади. На этом принципе и основаны все методы численного интегрирования. Отличительной особенностью каждого является различие в представлении только одной стороны элементарной криволинейной трапеции, множество которых дает суммарную площадь.

Численное интегрирование способом квадратуры можно осуществить несколькими весьма несложными методами, в которых используется общая схема вычислений:

0) известна подынтегральная функция f(x) и отрезок интегрирования;

1) выбирается число п (иногда оно обязательно четное);

2) отрезок интегрирования 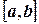разбивают на п частей одинаковой длины (шаг разбиения):

;

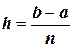3) на каждом шаге разбиения выбирают узлы

;

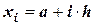4) вычисляют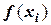

				…..
				…..

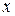
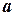
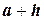
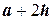
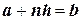
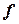
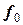
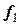
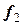
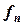
5) значения 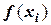подставляют в правую часть квадратурной формулы вида:

.

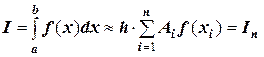Так как вычисления всегда носят приближенный характер, существует ошибка 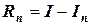такая, что 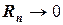при 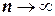. Это означает, что чем меньше шаг разбиения, тем квадратурная формула точнее. Следовательно, при решении задачи численного интегрирования с заданной точностью 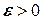необходимо найти 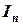так, чтобы в результате 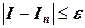. Этого можно добиться, подбирая соответствующее число разбиений п. Когда вся информация о функции f представлена таблично, сама постановка задачи интегрирования предполагает использование численных методов. На основе таблицы строят аппроксимирующую функцию и затем по ней вычисляют приближенное значение определенного интеграла.