Формула трапеций

При этом способе после разбиения отрезка интегрирования 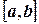на п равных участков функция f(x) кусочно интерполируется на каждом участке. В результате криволинейная трапеция заменяется соответствующим количеством прямолинейных трапеций, суммарная площадь которых и есть приближенное значение интеграла f(x) на отрезке 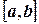(см. рисунок 24).

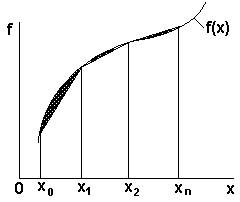
Рисунок 24 - К выводу формулы трапеций

Выведем квадратурную формулу приближенного интегрирования. Запишем значения площадей элементарных прямоугольных трапеций в последовательности:

;

;

;

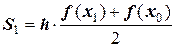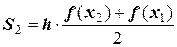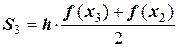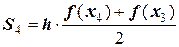
и просуммируем их.

.

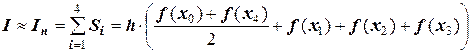Очевидно, квадратурная формула трапеций будет иметь общий вид:

.

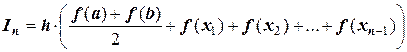Формула имеет и другое написание:

,

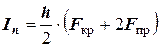где 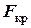- сумма значений функции в крайних точках,

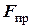- сумма значений функции в промежуточных точках.

Погрешность вычислений по формуле трапеций рассчитывается по выражению:

,

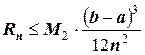где ,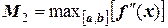

т.е. максимум второй производной на всем отрезке интегрирования. Обычно эти производные достаточно вычислить на концах отрезка интегрирования.

Видим, что погрешность метода трапеций практически такая же, как и при методе прямоугольников с центральной ординатой.