
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Элементы теории обыкновенных дифференциальных уравнений
|
|
Обыкновенным дифференциальным уравнением (ОДУ) называется уравнение:
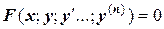 ,
,
которое связывает независимую переменную х, искомую функцию у(х) и ее производные вплоть до п -го порядка. Порядком ОДУ называется порядок старшей производной от искомой функции. Различают линейные и нелинейные дифференциальные уравнения. Например, линейное уравнение:
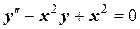
и нелинейное
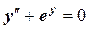 .
.
Так как элементами дифференциального уравнения являются производные функции у(х), которая и будет решением уравнения, то вполне очевиден основной принцип решения – интегрирование уравнения. Например, наиболее простая форма уравнения 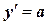 , где а=const, представляется так:
, где а=const, представляется так:
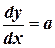 .
.
Разделяем переменные: 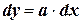 .
.
Интегрируем обе чести: 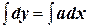 ,
,
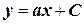 .
.
Напомним, что C=const и носит название постоянной интегрирования. Таким образом, конечное уравнение 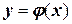 описывает бесконечное множество решений, которые геометрически представляют собой набор прямых (в рамках рассмотренного примера) линий с одинаковым угловым коэффициентом (а), но с произвольными значениями постоянной интегрирования С (рисунок 25).
описывает бесконечное множество решений, которые геометрически представляют собой набор прямых (в рамках рассмотренного примера) линий с одинаковым угловым коэффициентом (а), но с произвольными значениями постоянной интегрирования С (рисунок 25).
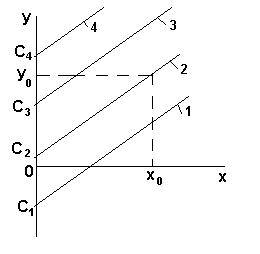
Рисунок 25 - Графическая интерпретация решения уравнения 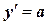
Чтобы выбрать из множества возможных решений необходимое (т.е. однозначно определить решение), необходимо задать координаты хотя бы одной точки на графике 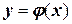 , например,
, например, 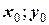 (заметим, что и для одного
(заметим, что и для одного 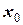 можно задать любое значение
можно задать любое значение  ). Зная величины
). Зная величины 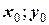 , можно легко найти постоянную интегрирования из условия: при
, можно легко найти постоянную интегрирования из условия: при 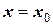 обязательно
обязательно 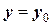 (прямая 2, рисунок 25). Тогда
(прямая 2, рисунок 25). Тогда
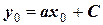 ,
,
отсюда 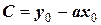 .
.
В результате получим окончательное решение:
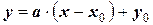 .
.
Общим интегралом дифференциального уравнения п -го порядка называют функцию 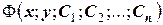 , которая связывает независимую переменную х, искомую функцию
, которая связывает независимую переменную х, искомую функцию 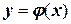 и п постоянных интегрирования
и п постоянных интегрирования 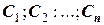 с помощью уравнения Ф=0. Функция
с помощью уравнения Ф=0. Функция 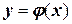 входит в интеграл неявным образом. Общим решением ОДУ называется функция
входит в интеграл неявным образом. Общим решением ОДУ называется функция 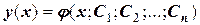 , связывающая независимую переменную и п постоянных интегрирования, т.е. она явно определяет функцию у(х).
, связывающая независимую переменную и п постоянных интегрирования, т.е. она явно определяет функцию у(х).
Как было показано выше, для определения постоянных надо задать дополнительные условия. Их число должно быть равно числу постоянных интегрирования (т.е. п – порядку дифференциального уравнения). После их определения получаем частное решение 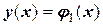 . Совокупность ОДУ (например, при п=1)
. Совокупность ОДУ (например, при п=1) 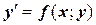 и дополнительных условий (в дальнейшем они будут называться начальными условиями) например, при
и дополнительных условий (в дальнейшем они будут называться начальными условиями) например, при 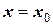 ,
, 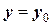 называют задачей Коши. Если дополнительные условия задаются более чем в одной граничной точке расчетной области, то совокупность ОДУ и дополнительных условий называют краевой задачей, а дополнительные условия - граничными или краевыми условиями.
называют задачей Коши. Если дополнительные условия задаются более чем в одной граничной точке расчетной области, то совокупность ОДУ и дополнительных условий называют краевой задачей, а дополнительные условия - граничными или краевыми условиями.
Актуальность задачи Коши для многих областей науки и техники явилась причиной разработки для ее решения большого количества методов. Они могут быть подразделены на две группы численных методов решения задачи Коши:
- одношаговые методы - для нахождения решения в некоторой точке отрезка используется информация только в одной предыдущей точке (к ним относятся методы Эйлера и Рунге-Кутты);
- многошаговые методы – для отыскания решения в некоторой точке используется информация о решении в нескольких предыдущих точках (методы Адамса).