Расчет погрешностей интегрирования методом двойного пересчета

Выше были приведены формулы строгой оценки погрешностей квадратурных формул. Они пригодны только при аналитически заданной подынтегральной функции и требуют нахождения максимума модуля производных, что обычно является сложной задачей. Существует не связанный с вычислением производных способ оценки погрешностей, применяемый и для интегралов от табличных функций. Это так называемый метод двойного пересчета или метод Рунге. Рассмотрим его применительно к формулам прямоугольников с левыми или правыми ординатами.

Выбираем некоторое натуральное число п и проводим вычисления по квадратурной формуле дважды:

- при разбиениях отрезка 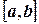на п участков с шагом 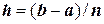(обозначим результат расчета через );

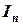- при разбиениях отрезка 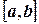на 2п участков с шагом 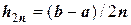(результат расчета ).

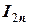Ясно, что лучшим приближением будет второй результат, т.е. 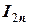, который и следует в дальнейшем считать приближенным значением интеграла. Погрешность вычисления будет равна:

для первого случая ,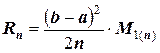

для второго случая .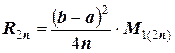

Строго говоря, 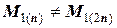как максимальное значение первой производной. Но в силу малости их различия принимают 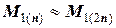и тогда получаем:

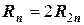
Иначе, удвоив количество отрезков разбиения, мы вдвое снижаем погрешность вычисления. Если к тому же запишем очевидные равенства

,

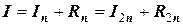получаем ;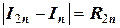

.

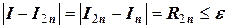Аналогичные формулы можно получить и для других квадратурных формул. Тогда, например, для формулы трапеций и формулы прямоугольников с центральными ординатами имеем:

, ;

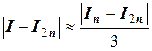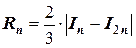для формулы Симпсона

, .

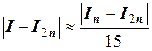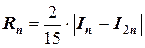Для применения метода Рунге в случае, когда данные для квадратурных формул берутся из таблицы значений подынтегральной функции, необходимо, чтобы таблица была с постоянным шагом и имела на отрезке 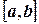сетку аргументов, достаточную для выбора узлов квадратуры, соответствующих шагам 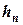и 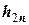.