Формула Симпсона

От квадратурной формулы следует ожидать большей точности, если для приближения подынтегральной функции использовать кусочно-квадратичную, т.е. нелинейную интерполяцию по трем точкам. В таком случае на этом участке истинная функция заменяется также криволинейной, но легко интегрируемой функцией. Последняя безусловно будет более близкой к истинной по сравнению, например, с линейной функцией, а соответственно и интегрирование выполненяется с меньшей ошибкой.

Разобьем отрезок 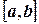на п равных участков точками 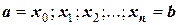с длиной 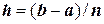, но теперь число п надо выбирать обязательно четным. Обозначим 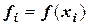. Тогда можно рассматривать “сдвоенные” отрезки 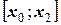; ; 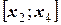…; 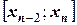как отрезки с тремя известными узлами, на каждом из которых можно получить интерполяционный многочлен Ньютона второй степени. Для 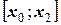он имеет вид:

.

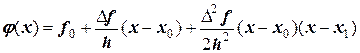Построим таблицу конечных разностей (таблица 23).

Таблица 23 - Таблица конечных разностей для двух участков

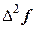
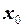
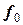
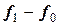
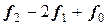
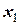
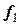
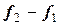
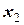
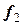
Введем новую переменную

.

Тогда можно записать

; .

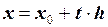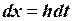Так как ,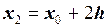

то при ; ;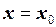

; .

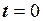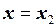
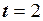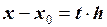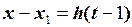В результате получим следующую редакцию многочлена Ньютона для участка :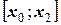

.

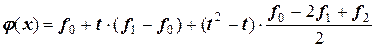На этом участке можем вычислить определенный интеграл:

,

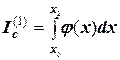или, заменяя переменную:

.

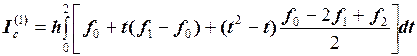В результате простых вычислений получим:

.

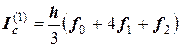Получили так называемую малую формулу Симпсона, предназначенную для приближенного интегрирования функции путем ее замены функцией параболы . Она вполне приемлема, если первичная функция достаточно пологая.

Процедура кусочно-квадратической интерполяции может быть продолжена на последующие участки, но от этого структура формулы Симпсона не изменится. Многократное ее применение даст следующую последовательность:

для участка ;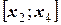

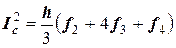для участка ;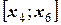

……………………………………………………

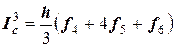для участка ;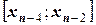

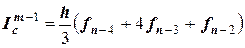для участка ;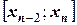

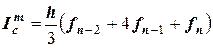где .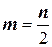

Определенный интеграл от функции на участке 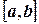заменяется приближенным интегралом:

,

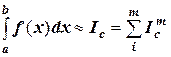или ,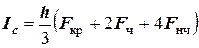

где -сумма крайних ординат;

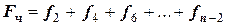- сумма четных ординат;

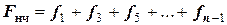- сумма нечетных ординат.

Получили полную квадратичную формулу Симпсона. Погрешность вычисления по этой формуле можно рассчитать по выражению:

,

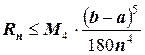где .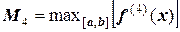

Формула Симпсона выглядит более громоздкой по сравнению с формулами прямоугольников и трапеций, но она значительно точнее их и может привести к требуемому результату при меньших п.