Метод Эйлера

Имеется исходное ОДУ первого порядка вида 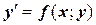, причем при 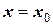; 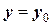. Если точным решением этого уравнения является функция , то это уравнение записывается в виде тождества . В случае применения численных методов решение находится в виде приближения. Для этого, как правило, применяют конечно-разностный метод (или метод сеток), согласно которому весь отрезок определения функции разбивается на п участков с шагом

,

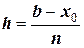где х₀ и b – начало и конец отрезка определения конечной функции. Тогда расчетными точками будут

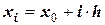, где .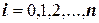

Целью приближенного решения ОДУ будет нахождение таблицы вида

Таблица 24 – Табличная запись решения ОДУ

				….
				….

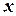
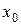
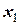
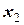
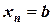
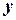
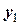
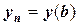
В этой таблице определена полностью только одна (первая) точка 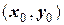. Рассмотрим два подхода к решению поставленной задачи.

Геометрический метод. Предположим, что функция найдена. График этой функции обязательно должен пройти через точку 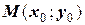, рисунок 27. Необходимо теоретически определить очередную точку N.

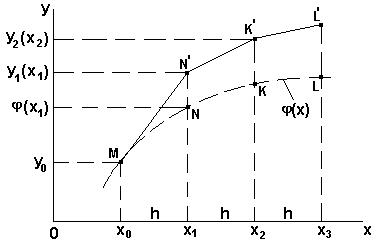
Рисунок 27 - К обоснованию метода решения дифференциального уравнения

Пользуясь тем, что в точке х₀ известно значение 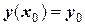и значение производной , можно записать уравнение касательной (прямой линии) к графику искомой функции в точке :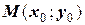

.

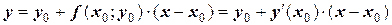Это уравнение прямой МN’. При достаточно малом шаге h=х₁–х₀ ордината

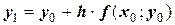
будет мало отличаться от 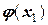, т.е. за результат первого шага расчетов принимают не точку N (истинное значение 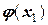), а точку 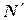, но с определенной ошибкой положения. Затем, опираясь на параметры точки 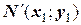, проводят через нее линию, описываемую уравнением:

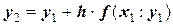
и получают соответственно точку 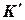как очередное приближение к точке К. В итоге этого процесса, определяемого формулой

,

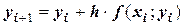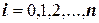
и называемого методом Эйлера, график решения 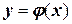данной задачи Коши приближенно представляется ломаной, составленной из отрезков приближенных касательных, откуда происходит другое название метода – метод ломаных.

Квадратурный способ. Как было показано выше, начальную задачу решения ОДУ можно записать следующим образом.

Запишем первичное ОДУ 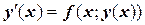или 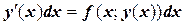. Проинтегрируем левую и правую части на участке от х₀ до х₁:

.

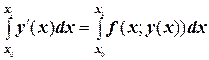Отсюда, учитывая, что для 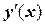первообразной является функция , получим

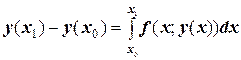
или .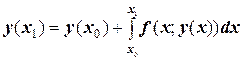

Таким образом, исходное дифференциальное уравнение с начальным условием преобразовалось в интегральное уравнение, где неизвестная функция входит под знак интеграла. Применим к интегралу в правой части равенства квадратурную формулу приближенного вычисления интеграла методом прямоугольников, например, с левой ординатой:

;

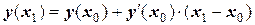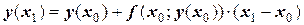
или .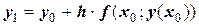

Повторяя пошагово процедуру вычислений, мы так же получим расчетную формулу Эйлера:

, .

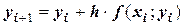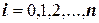Задача 21. Даны ОДУ 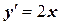и начальные условия 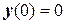, т.е при х=х₀=0; у(х₀)=0. Найти методом Эйлера численное решение задачи Коши на отрезке 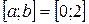с шагом .

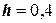Решение. Используя начальные условия, находим:

;

;

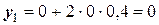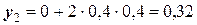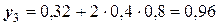и так далее.

Одновременно можно получить и точное решение:

; ; ; .

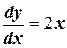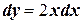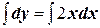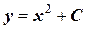Постоянную интегрирования найдем из начальных условий. Очевидно, что С=0. Тогда окончательно 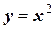. Обозначим 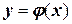и при различных 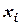рассчитаем 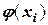. Результаты приближенных и точных расчетов запишем в таблицу 25, где 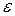- пошаговая погрешность вычисления.

Таблица 25 - Расчетная таблица при решении уравнения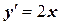

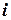
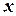
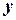
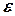
	0, 4 0, 8 1, 2 1, 6 2, 0	0, 32 0, 96 1, 92 3, 20	0, 16 0, 64 1, 44 2, 56 4, 0	0, 16 0, 32 0, 48 0, 64 0, 80

Она оказывается достаточно большой, но это в значительной степени объясняется крупным шагом. Кроме того, характерно, что абсолютная погрешность растет по мере приближения к правой границе интегрирования. Уже первая приближенная точка 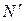(см. рисунок 27) не совпадает с ее точным положением. Безусловно тенденция несовпадения сохранится и для последующих точек. Поэтому именно суммирование пошаговых ошибок и заметно по величине .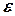