Дифференциальных уравнений

Рассмотренные выше методы Эйлера и его модификации принадлежат к семейству так называемых методов Рунге-Кутты. Они многочисленны и основной целью совершенствования методов является повышение точности вычислений. При построении численного решения задачи Коши (как это было показано выше в задаче 21) происходит накапливание погрешности. Они имеют различные источники. Поэтому строгие оценки погрешностей чисел 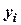вида 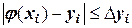оказываются сложными и неинформативными. На практике ими не пользуются, а ограничиваются ориентировочной оценкой точности и нахождением приближенных значений для расстояний 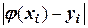по правилу Рунге (метод двойного пересчета).

Пусть строится таблица с шагом h. Сначала одним из расчетных методов находятся значения 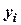(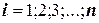) с шагом h, а затем проводятся аналогичные вычисления с шагом 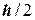. Соответствующие аргументам 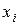новые табличные значения обозначим через 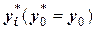. Это улучшенные приближения к 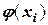и поэтому таблицу с данными 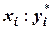берут в качестве искомого численного решения с шагом h.

Расстояния между 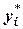и точными числами 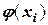вычисляют по приближенным формулам:

для метода Эйлера: ;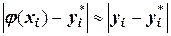

для обеих модификаций метода Эйлера: 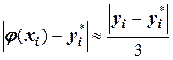.