Метод Эйлера-Коши

Рассмотрим две модификации метода Эйлера, разработка которых преследовала цель снизить накопительную погрешность вычислений. При этом в дополнение к условиям задачи Коши будем считать, что все частные производные второго порядка функции 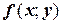непрерывны в области вычислений. Тогда и решение имеет непрерывную третью производную. Вычислительные формулы будем выводить двумя способами: геометрически и аналитически. Геометрические рассуждения наглядны, а аналитические выкладки позволяют охарактеризовать точность методов.

Метод Эйлера с пересчетом. Проведем следующие геометрические построения. Пусть известны данные 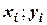и 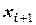(например, 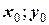и ).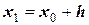

Точка 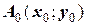лежит на некоторой интегральной кривой - точном решении задачи Коши (рисунок 28). Пользуясь вышеописанным методом Эйлера, найдем при 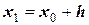вторую точку приближения 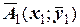, где

.

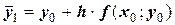Обозначим 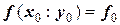. При методе Эйлера процесс приближения продолжался бы далее, но в данном случае положение точки 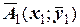будет использовано для получения указания на направление еще одной касательной, т.е. той, которую мы бы провели в точке 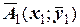. Поэтому далее вычисляют 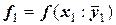, но используют 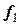как корректирующий компонент, уточняющий направление касательной в точке 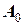. Коррекцию производят методом усреднения, а именно рассчитывают:

.

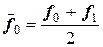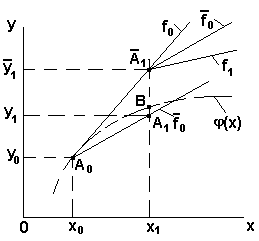
Рисунок 28 - К обоснованию метода Эйлера-Коши

Это направление и принимается для касательной, проводимой из левой (на исследуемом отрезке) точки. Тогда записываем ординату точки :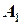

.

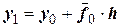Далее процесс будет продолжен. Следовательно, алгоритм вычислений методом пересчета будет следующий:

- известны исходные данные , ;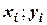

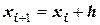- вычисляют ;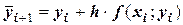

- вычисляют ;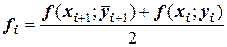

- вычиляют ;

- очередная итерационная точка определена координатами .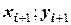

Задача 22. Получить решение ОДУ 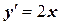, пользуясь результатами предыдущей задачи.

Решение. Составим расчетную таблицу для реализации метода Эйлера-Коши. Такой прием часто используют для формального представления полного алгоритма решения. Очень часто в таблицу вписывают и расчетные выражения. Ниже приведена подобная расчетная таблица. Шаг разбиения отрезка вычислений .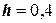

Таблица 26 - Расчетная таблица к решению ОДУ 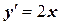методом Эйлера-Коши

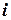
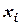
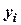
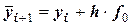
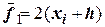
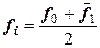
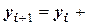
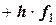
					0, 8	0, 4	0, 16
	0, 4	0, 16	0, 8	0, 48	1, 6	1, 2	0, 64
	0, 8	0, 64	1, 6	1, 28	2, 4	2, 0	1, 44
	1, 2	1, 44	2, 4	2, 4	3, 2	2, 8	2, 56
	1, 6	2, 56	3, 2	2, 88	4, 0	3, 6	4, 0
	2, 0	4, 0	4, 0	-	-	-	-

Видим, что для заданного ОДУ уже методом Эйлера-Коши получено его точное решение. Безусловно, далеко не всегда это удается.

Метод срединных точек. Как и в предыдущем случае, решение получим геометрическим способом. Напомним, что в принципе речь идет о том, каким образом ввести коррекцию на вычисление тангенсов углов наклона касательных, рассчитываемых в левых границах очередного участка итерационных вычислений. В рассматриваемом методе поиск точки 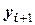ведется в направлении касательной, тангенс угла которой рассчитывается для точки, лежащей на середине отрезка 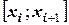, т.е. абсциссой этой точки будет 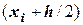. Алгоритм вычислений следующий:

- имеются исходные данные ; ; ;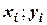

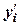- рассчитывают ординату срединной точки

;

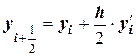- рассчитывают тангенс угла наклона касательной в срединной точке:

;

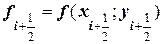- рассчитывают ординату новой точки

.

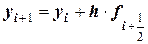Этот алгоритм представлен на рисунке 29.

Рисунок 29 - К выводу метода срединных точек

Срединной точкой является 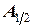. Угловой коэффициент касательной к интегральной кривой, проходящей через эту точку, равен 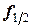. Затем эта касательная переносится и проводится через точку 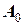и затем, уже при 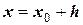получают точку 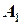. Из рисунка 29 видно, что, если следовать методу Эйлера, вторая итерационная расчетная точка была бы . Безусловно, проведенная коррекция угла наклона позволила снизить ошибку.

Задача 23. Для задачи 22 найти решение методом срединных точек.

Решение. Как и в предыдущем случае, все промежуточные результаты расчетов представим в табличной форме.

Таблица 27 - Расчетная таблица к решению ОДУ 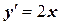методом срединных точек

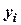
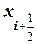
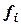
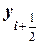
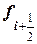
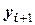
			0, 2			0, 4	0, 16
	0, 4	0, 16	0, 6	0, 8	0, 32	1, 2	0, 64
	0, 8	0, 64	1, 0	1, 6	0, 96	2, 0	1, 44
	1, 2	1, 44	1, 4	2, 4	1, 92	2, 8	2, 56
	1, 6	2, 56	1, 8	3, 2	3, 2	3, 6	4, 0
	2, 0	4, 0	-	-	-	-	-

В таблице представлены данные, полученные по следующим расчетным зависимостям:

1) ;

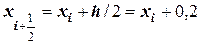2) ;

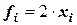3) ;

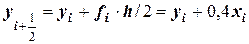4) ;

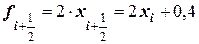5) .

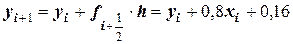Видно, что и этот метод решения дает значительно более точные (в данном случае абсолютно точные) результаты по сравнению с исходным методом Эйлера.