
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула прямоугольников
|
|
Сущность принципа квадратуры при численном интегрировании рассмотрена выше. Иначе – вычислить определенный интеграл означает вычислить площадь нелинейной трапеции. Численным методом это, например, можно сделать следующим образом. Отрезок 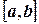 разбивают на п равных частей и на каждом из участков разбиения строят, например, прямоугольник, площадь
разбивают на п равных частей и на каждом из участков разбиения строят, например, прямоугольник, площадь
каждого из которых будет равна:
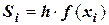 .
.
Тогда 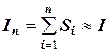 .
.
Разбиение криволинейной трапеции на прямоугольники может быть выполнена тремя способами.
1) В качестве 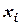 выбирают левую границу участка разбиения. Тогда
выбирают левую границу участка разбиения. Тогда
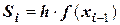
и 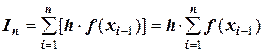 .
.
Графически этот способ представлен для нисходящей и восходящей функций, на рисунке 21а, б, соответственно.
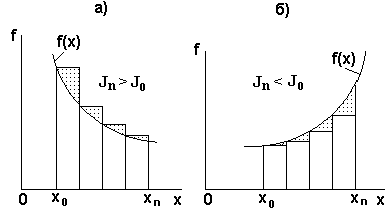
Рисунок 21 - К выводу формулы прямоугольников с левыми ординатами
2) В качестве 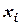 выбирают правую границу участка разбиения. Тогда
выбирают правую границу участка разбиения. Тогда
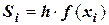
и 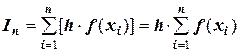 .
.
Графически этот способ представлен на рисунке 22.
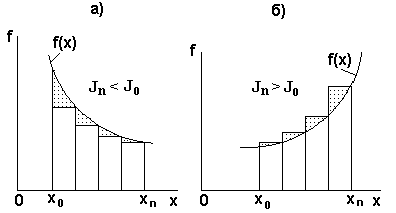
Рисунок 22 - К выводу формулы прямоугольников с правыми ординатами
Квадратурная формула первого типа называется формулой прямоугольников с левыми ординатами, а второго типа – формулой прямоугольников с правыми координатами.
3) В качестве 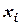 выбирают середину участка разбиения, т.е.
выбирают середину участка разбиения, т.е.
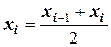 ,
,
и 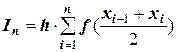 .
.
Графическая интерпретация способа представлена на рисунке 23. Квадратурная формула третьего типа называется формулой прямоугольников с центральными ординатами.
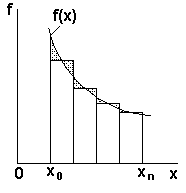
Рисунок 23 - К выводу формулы прямоугольников с центральной ординатой
Как видно из графических построений, в любом случае возникает погрешность вычислений (заштрихованные зоны). Величина и знак погрешности зависит от подынтегральной функции, от величины отрезка интегрирования и количества участков разбиения п. Для интегрирования по формулам прямоугольников с правыми или левыми ординатами погрешность вычислений определяется по формуле:
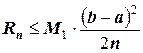 ,
,
где 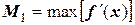 ,
,
т.е. максимальное значение первой производной функции f(x) на участке интегрирования. Если функция задана таблично, то это максимальное (абсолютное) значение конечной разности первого порядка.
Для интегрирования по формуле прямоугольников с центральными ординатами погрешность вычислений определяется по формуле:
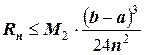 ,
,
где 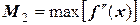 ,
,
т.е. максимум второй производной функции на участке интегрирования (максимум конечной разности второго порядка). Несомненно, интегрирование по третьему методу дает более низкую погрешность.